Dynamic, Absolute, and Kinematic Viscosity – Definitions & Conversions
The differences between dynamic, absolute, and kinematic viscosity - a fluids resistance to flow - with definitions, unit conversions, and practical applications for engineers and scientists.
Viscosity is an important fluid property when analyzing liquid behavior and fluid motion near solid boundaries. The viscosity of a fluid is a measure of its resistance to gradual deformation by shear stress or tensile stress. The shear resistance in a fluid is caused by inter-molecular friction exerted when layers of fluid attempt to slide by one another.
- viscosity is the measure of a fluid's resistance to flow
- molasses is highly viscous
- water is medium viscous
- gas is low viscous
There are two related measures of fluid viscosity
- dynamic ( or absolute )
- kinematic
Dynamic (absolute) Viscosity
Absolute viscosity - coefficient of absolute viscosity - is a measure of internal resistance. Dynamic (absolute) viscosity is the tangential force per unit area required to move one horizontal plane with respect to an other plane - at an unit velocity - when maintaining an unit distance apart in the fluid.
The shearing stress between the layers of a non turbulent fluid moving in straight parallel lines can be defined for a Newtonian fluid as
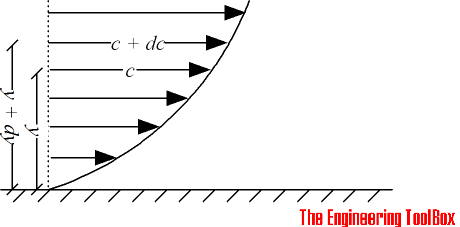
Shear stress can be expressed
τ = μ dc / dy
= μ γ (1)
where
τ = shearing stress in fluid (N/m2)
μ = dynamic viscosity of fluid (N s/m2)
dc = unit velocity (m/s)
dy = unit distance between layers (m)
γ = dc / dy = shear rate (s-1)
Equation (1) is known as the Newtons Law of Friction.
(1) can be rearranged to express Dynamic viscosity as
μ = τ dy / dc
= τ / γ (1b)
In the SI system the dynamic viscosity units are N s/m2, Pa s or kg/(m s) - where
- 1 Pa s = 1 N s/m2 = 1 kg/(m s) = 0.67197 lbm/(ft s) = 0.02088 slug /(ft s) = 0.02089 lbf s/ft2
Dynamic viscosity may also be expressed in the metric CGS (centimeter-gram-second) system as g/(cm s) , dyne s/cm 2 or poise (p) where
- 1 poise = 1 dyne s/cm2 = 1 g/(cm s) = 1/10 Pa s = 1/10 N s/m2
For practical use the Poise is normally too large and the unit is therefore often divided by 100 - into the smaller unit centipoise (cP) - where
- 1 P = 100 cP
- 1 cP = 0.01 poise = 0.01 gram per cm second = 0.001 Pascal second = 1 milliPascal second = 0.001 N s/m2
Water at 20.2 oC (68.4 oF) has the absolute viscosity of one - 1 - centiPoise.
| Liquid | Absolute Viscosity*) (N s/m2, Pa s) |
|---|---|
| Air | 1.983×10-5 |
| Water | 10-3 |
| Olive Oil | 10-1 |
| Glycerol | 100 |
| Liquid Honey | 101 |
| Golden Syrup | 102 |
| Glass | 1040 |
*) at room temperature
Kinematic Viscosity
Kinematic viscosity is the ratio of - absolute (or dynamic) viscosity to density - a quantity in which no force is involved. Kinematic viscosity can be obtained by dividing the absolute viscosity of a fluid with the fluid mass density like
ν = μ / ρ (2)
where
ν = kinematic viscosity (m2/s)
μ = absolute or dynamic viscosity (N s/m2)
ρ = density (kg/m3)
In the SI-system the theoretical unit of kinematic viscosity is m2/s - or the commonly used Stoke (St) where
- 1 St (Stokes) = 10-4 m2/s = 1 cm2/s
Stoke comes from the CGS (Centimetre Gram Second) unit system.
Since the Stoke is a large unit it is often divided by 100 into the smaller unit centiStoke (cSt) - where
- 1 St = 100 cSt
- 1 cSt (centiStoke) = 10-6 m2/s = 1 mm2/s
- 1 m2/s = 106 centiStokes
The specific gravity for water at 20.2 oC (68.4 oF) is almost one, and the kinematic viscosity for water at 20.2 oC (68.4 oF) is for practical purpose 1.0 mm2/s ( cStokes). A more exact kinematic viscosity for water at 20.2 oC (68.4 oF) is 1.0038 mm2/s (cSt).
A conversion from absolute to kinematic viscosity in Imperial units can be expressed as
ν = 6.7197×10-4 μ / γ (2a)
where
ν = kinematic viscosity (ft2/s)
μ = absolute or dynamic viscosity (cP)
γ = specific weight (lb/ft3)
Viscosity and Reference Temperature
The viscosity of a fluid is highly temperature dependent - and for dynamic or kinematic viscosity to be meaningful the reference temperature must be quoted. In ISO 8217 the reference temperature for a residual fluid is 100 oC. For a distillate fluid the reference temperature is 40 oC .
- for a liquid - the kinematic viscosity decreases with higher temperature
- for a gas - the kinematic viscosity increases with higher temperature
Related Mobile Apps from The Engineering ToolBox 
This is a free app that can be used offline on mobile devices.
Other Viscosity Units
Saybolt Universal Seconds (or SUS, SSU)
Saybolt Universal Seconds (or SUS) is an alternative unit for measuring viscosity. The efflux time is Saybolt Universal Seconds (SUS) required for 60 milliliters of a petroleum product to flow through the calibrated orifice of a Saybolt Universal viscometer - under a carefully controlled temperature and as prescribed by test method ASTM D 88. This method has largely been replaced by the kinematic viscosity method. Saybolt Universal Seconds is also called the SSU number (Seconds Saybolt Universal) or SSF number (Saybolt Seconds Furol) .
Kinematic viscosity in SSU versus dynamic or absolute viscosity can be expressed as
νSSU = B μ / SG
= B νcentiStokes (3)
where
νSSU = kinematic viscosity (SSU)
B = 4.632 for temperature 100 oF (37.8 oC)
B = 4.664 for temperature 210 oF (98.9 oC)
μ = dynamic or absolute viscosity (cP)
SG = Specific Gravity
νcentiStokes = kinematic viscosity (centiStokes)
Degree Engler
Degree Engler is used in Great Britain as a scale to measure kinematic viscosity. Unlike the Saybolt and Redwood scales, the Engler scale is based on comparing the flow of the substance being tested to the flow of another substance - water. Viscosity in Engler degrees is the ratio of the time of a flow of 200 cubic centimeters of the fluid whose viscosity is being measured - to the time of flow of 200 cubic centimeters of water at the same temperature (usually 20 oC but sometimes 50 oC or 100 oC) in a standardized Engler viscosity meter.
Newtonian Fluids
A fluid where the shearing stress is linearly related to the rate of shearing strain - is designated as a Newtonian Fluid.
A Newtonian material is referred to as true liquid since the viscosity or consistency is not affected by shear such as agitation or pumping at a constant temperature. Most common fluids - both liquids and gases - are Newtonian fluids. Water and oils are examples of Newtonian liquids.
Shear-thinning or Pseudo-plastic Fluids
A Shear-thinning or pseudo-plastic fluid is a fluid where the viscosity decrease with increased shear rate. The structure is time-independent.
Thixotropic Fluids
A Thixotropic fluid has a time-dependent structure. The viscosity of a thixotropic fluid decreases with increasing time - at a constant shear rate.
Ketchup and mayonnaise are examples of thixotropic materials. They appear thick or viscous but are possible to pump quite easily.
Dilatant Fluids
A Shear Thickening Fluid - or Dilatant Fluid - increases the viscosity with agitation or shear strain. Dilatant fluids are known as non-Newton fluids.
Some dilatant fluids can become almost solid in a pump or pipe line. With agitation cream becomes butter and candy compounds. Clay slurry and similar heavily filled liquids do the same thing.
Bingham Plastic Fluids
A Bingham Plastic Fluid has a yield value which must be exceeded before it will start to flow like a fluid. From that point the viscosity decreases with increasing agitation. Toothpaste, mayonnaise and tomato ketchup are examples of such products.
Example - Air, Convert between Kinematic and Absolute Viscosity
Kinematic viscosity of air at 1 bar (1×105 Pa, N/m2) and 40 oC is 16.97 cSt (16.97×10-6 m2/s) .
The density of the air can be estimated with the Ideal Gas Law
ρ = p / (R T)
= (1×105 N/m2) / ( (287 J/(kg K)) ((273 oC) + (33 oC)))
= 1.113 (kg/m3)
where
ρ = density (kg/m3)
p = absolute pressure (Pa, N/m2)
R = individual gas constant (J/(kg K))
T = absolute temperature (K)
The absolute viscosity can be calculated as
μ = 1.113 (kg/m3) 16.97×10-6 (m2/s)
= 1.88 10-5 (kg/(m s), N s/m2)
Viscosity of some Common Liquids
| centiStokes (cSt, 10-6 m2/s, mm2/s) | Saybolt Second Universal (SSU, SUS) | Typical liquid |
|---|---|---|
| 0.1 | Mercury | |
| 1 | 31 | Water (20 oC) |
| 4.3 | 40 | Milk SAE 20 Crankcase Oil SAE 75 Gear Oil |
| 15.7 | 80 | No. 4 fuel oil |
| 20.6 | 100 | Cream |
| 43.2 | 200 | Vegetable oil |
| 110 | 500 | SAE 30 Crankcase Oil SAE 85 Gear Oil |
| 220 | 1000 | Tomato Juice SAE 50 Crankcase Oil SAE 90 Gear Oil |
| 440 | 2000 | SAE 140 Gear Oil |
| 1100 | 5000 | Glycerine (20 oC) SAE 250 Gear Oil |
| 2200 | 10000 | Honey |
| 6250 | 28000 | Mayonnaise |
| 19000 | 86000 | Sour cream |
Kinematic viscosity can be converted from SSU to Centistokes with
νCentistokes = 0.226 νSSU - 195 / νSSU (4)
where
νSSU < 100
νCentistokes = 0.220 νSSU - 135 / νSSU
where
νSSU > 100
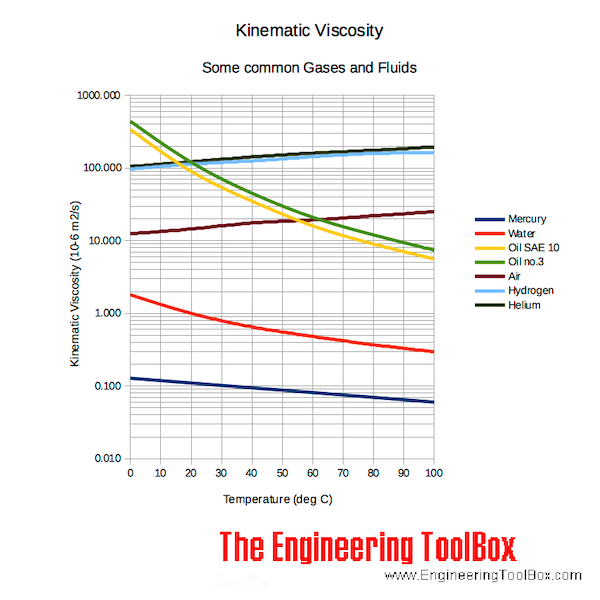
Viscosity and Temperature
Kinematic viscosity of fluids like water, mercury, oils SAE 10 and oil no. 3 - and gases like air, hydrogen and helium are indicated in the diagram below. Note that
- for liquids - viscosity decreases with temperature
- for gases - viscosity increases with temperature
Measuring Viscosity
Three types of devices are used to measure viscosity
- capillary tube viscometer
- Saybolt viscometer
- rotating viscometer
Related Searches
centipoises • centistokes • viscosity • dynamic viscosity • absolute viscosity • kinematic viscosity • viscosity units • viscosity conversion • fluid mechanics • engineering properties • viscosity formulas • viscosity tables •



