Beams - Fixed at One End and Supported at the Other - Continuous and Point Loads
Supporting loads, moments and deflections.
- Beams - Supported at Both Ends - Continuous and Point Loads
- Beams - Fixed at One End and Supported at the Other - Continuous and Point Loads
- Beams - Fixed at Both Ends - Continuous and Point Loads
Beam Fixed at One End and Supported at the Other - Single Point Load
Bending Moment
MA = - F a b (L + b) / (2 L2) (1a)
where
MA = moment at the fixed end (Nm, lbf ft)
F = load (N, lbf)
MF = Rb b (1b)
where
MF = moment at point of load F (Nm, lbf ft)
Rb = support load at support B (N, lbf)
Deflection
δF = F a3 b2 (3 L + b) / (12 L3 E I) (1c)
where
δF = deflection (m, ft)
E = Modulus of Elasticity (Pa (N/m2), N/mm2, psi)
I = Area Moment of Inertia (m4, mm4, in4)
Support Reactions
RA = F b (3 L2 - b2) / (2 L3) (1d)
where
RA = support force in A (N, lbf)
RB = F a2 (b + 2 L ) / (2 L3) (1f)
where
RB = support force in B (N, lbf)
Beam Fixed at One End and Supported at the Other - Continuous Load
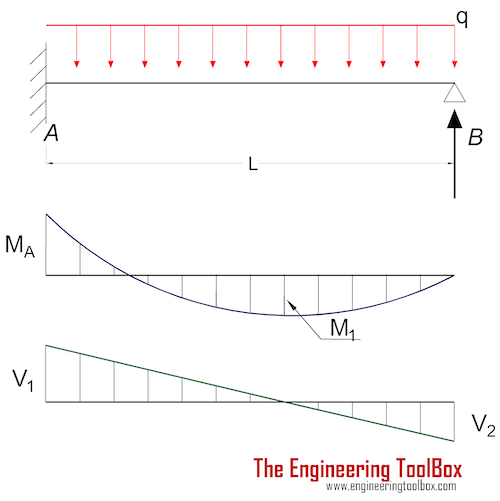Bending Moment
MA = - q L2 / 8 (2a)
where
MA = moment at the fixed end (Nm, lbf ft)
q = continuous load (N/m, lbf/ft)
M1 = 9 q L2 / 128 (2b)
where
M1 = maximum moment at x = 0.625 L (Nm, lbf ft)
Deflection
δmax = q L4 / (185 E I) (2c)
where
δmax = max deflection at x = 0.579 L (m, ft)
δ1/2 = q L4 / (192 E I) (2d)
where
δ1/2 = deflection at x = L / 2 (m, ft)
Support Reactions
RA = 5 q L / 8 (2e)
RB = 3 q L / 8 (2f)
Beam Fixed at One End and Supported at the Other - Continuous Declining Load
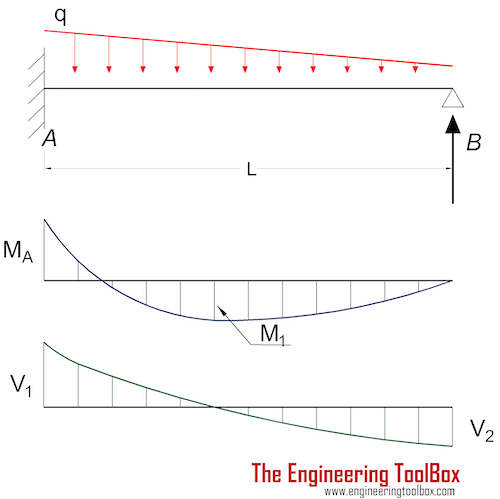Bending Moment
MA = - q L2 / 15 (3a)
where
MA = moment at the fixed end (Nm, lbf ft)
q = continuous declining load (N/m, lbf/ft)
M1 = q L2 / 33.6 (3b)
where
M1 = maximum moment at x = 0.553 L (Nm, lbf ft)
Deflection
δmax = q L4 / (419 E I) (3c)
where
δmax = max deflection at x = 0.553 L (m, ft)
δ1/2 = q L4 / (427 E I) (3d)
where
δ1/2 = deflection at x = L / 2 (m, ft)
Support Reactions
RA = 2 q L / 5 (3e)
RB = q L / 10 (3f)
Beam Fixed at One End and Supported at the Other - Moment at Supported End
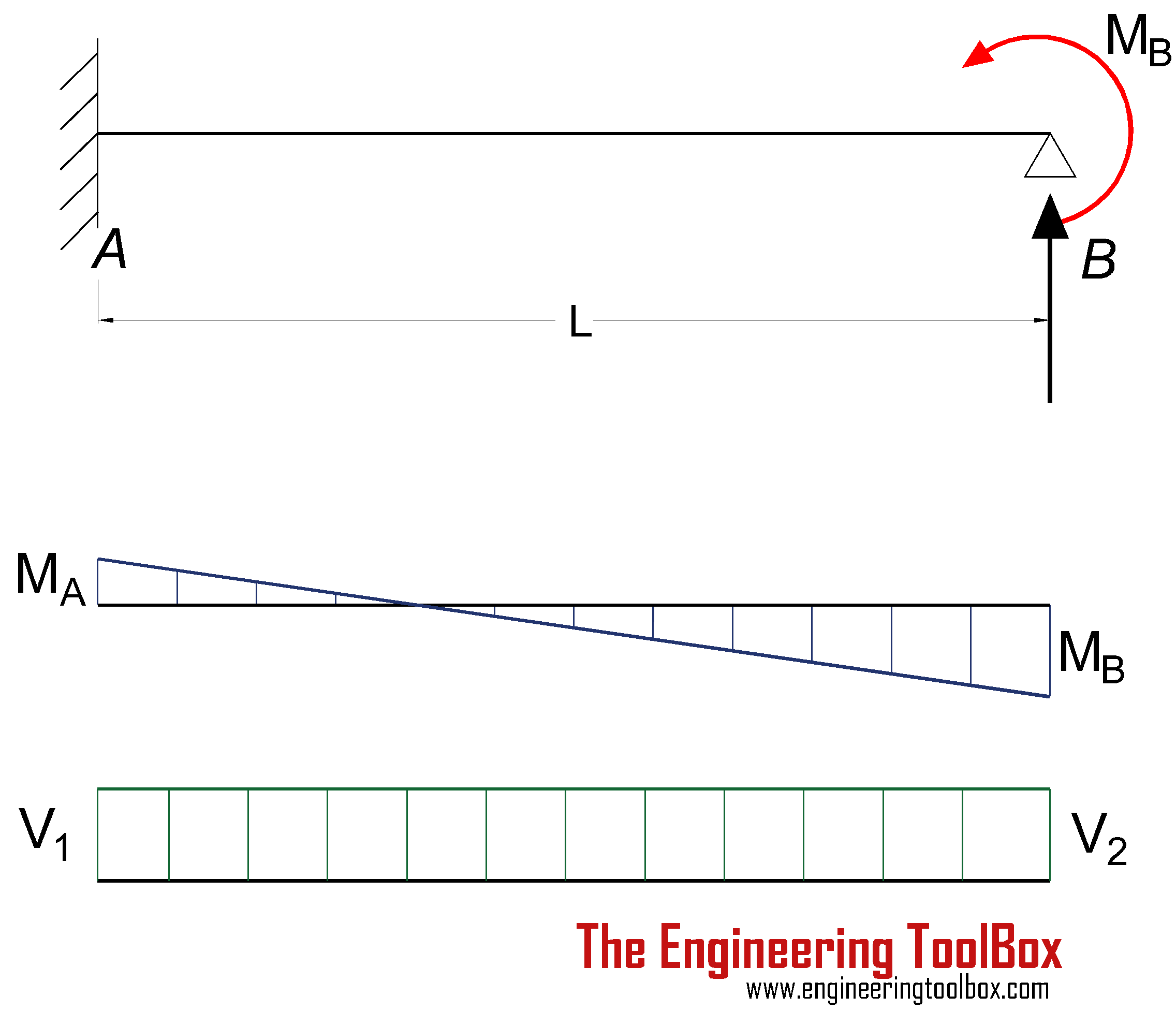Bending Moment
MA = -MB / 2 (4a)
where
MA = moment at the fixed end (Nm, lbf ft)
Deflection
δmax = MB L2 / (27 E I) (4b)
where
δmax = max deflection at x = 2/3 L (m, ft)
Support Reactions
RA = 3 MB / (2 L) (4c)
RB = - 3 MB / (2 L) (4d)
