Three-Hinged Arches - Continuous and Point Loads
Support reactions and bending moments.
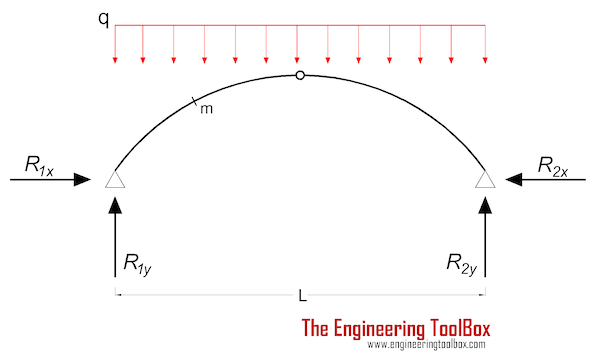
Three-Hinged Arch - Continuous Load
Bending Moment
Mm = (q L2 / 8) (4 (xm / L - (xm / L)2) - ym / yc) (1a)
where
Mm = moment at m (Nm, lbf ft)
q = continuous load (N/m, lbf/ft)
xm = x-coordinate for m (m, ft)
ym = y-coordinate for m (m, ft)
yc = y-coordinate for center hinge (m, ft)
L = horizontal distance between the supports (m, ft)
Cartesian coordinates related to a center located in the hinge of support no. 1.
Support Reactions
R1y = R2y
= q L / 2 (1b)
where
R = support force (N, lbf)
R1x = R2x
= q L2 / (8 yc) (1c)
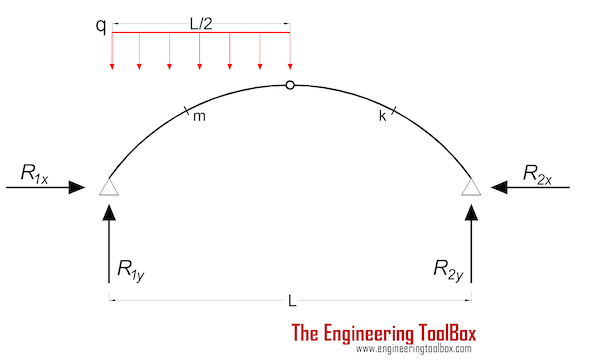
Three-Hinged Arch - Half Continuous Load
Bending Moment
Mm = (q L2 / 16) (8 (xm / L - (xm / L)2) - 2 xm / L - ym / yc) (2a)
Support Reactions
R1y = 3 q L / 8 (2b)
R2y = q L / 8 (2c)
R1x = R2x
= q L2 / (16 yc) (2d)
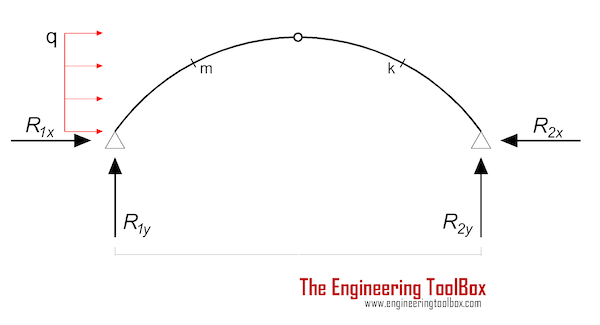
Three-Hinged Arch - Horizontal Continuous Load
Bending Moment
Mm = (q L2 / 2) (xm / L - 3 xm / L + (xm / L)2) (3a)
Mk = (q L2 / 4) (2 (L - xk) / L - yk / yc) (3b)
where
Mk = moment at k (Nm, lbf ft)
yk = y-coordinate for k (m, ft)
xk = x-coordinate for k (m, ft)
Support Reactions
R1y = - q yc2 / (2 L) (3c)
R2y = q yc2 / (2 L) (3d)
R1x = - 3 q yc / 4 (3e)
R2x = q yc / 4 (3f)
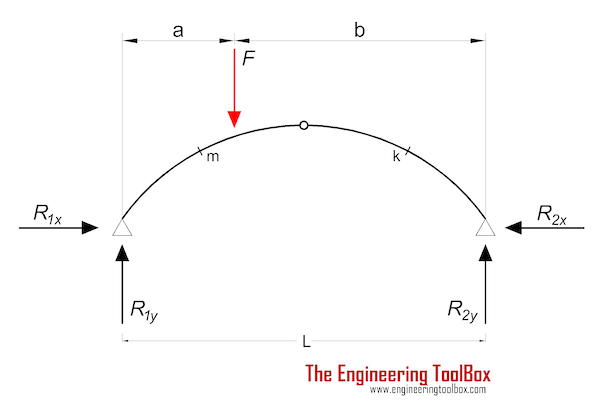
Three-Hinged Arch - Eccentric Point Load
Bending Moment
Mm = (F a / 2) (2 (b / a) (xm / L) - ym / yc) (4a)
Mk = (F a /2) (2 (L - xk) / L - yk / yc) (4b)
Support Reactions
R1y = F b / L (4c)
R2y = F a / L (4d)
R1x = R2x
= F a / (2 yc) (4f)
