Weight of Beams - Stress and Strain
Stress and deformation of vertical beams due to own weight.
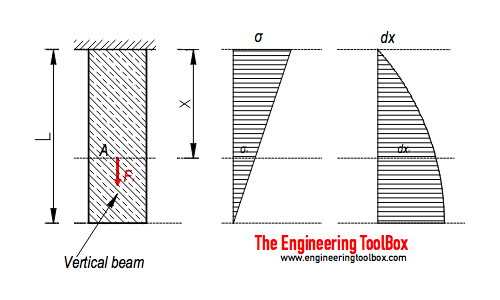
Axial Force
The axial force acting in a cross sectional area in distance x in a vertical beam due to it's own weight - can be calculated as
Fx = γ A (L - x) (1)
where
Fx = axial force in distance x (N)
y = specific weight - unit volume weight (N/m3)
A = cross-sectional area (m2)
L = length of beam (m)
x = distance (m)
The specific weight can be expressed as
y = ρ g (2)
where
ρ = density of beam (kg/m3)
g = acceleration of gravity (9.81 m/s2)
(1) can with (2) be modified to
Fx = ρ g A (L - x) (2b)
Axial Stress
The axial stress at a distance x can be calculated as
σx = Fx / A
= γ (L - x)
= ρ g (L - x) (3)
where
σx = axial stress (Pa, N/m2)
Note! - the cross-sectional area is irrelevant.
The axial stress at distance x = L
σx=L = γ (L - L)
= ρ g (L - L)
= 0 (3a)
The axial stress at distance x = 0
σx=0 = γ (L - 0)
= ρ g (L - 0)
= γ L
= ρ g L (3b)
Axial Deformation
The axial deformation at distance x can be calculated as
dxx = y x (2 L - x) / (2 E)
= ρ g x (2 L - x) / (2 E) (4)
where
dx = deformation (m)
E = modulus of elasticity (N/m2)
The axial deformation at distance x = L
dxx=L = y L2 / (2 E)
= ρ g L2 / (2 E) (4a)
The axial deformation at distance x = 0
dxx=0 = 0 (4b)
Example - Stress and Axial Deformation of a Vertical Steel Rod
A 45 m long steel rod with density 7280 kg/m3 and cross-sectional area 0.1 m2 is mounted as indicated in the figure above.
The maximum force acting in the rod at distance x = 0 m can be calculated with (1b)
Fx=0 = (7280 kg/m3) (9.81 m/s2) (0.1 m2) ((45 m) - (0 m))
= 321376 N
= 321 kN
The maximum axial stress in the rod at distance x = 0 m can be calculated (3b)
σx=0 = (7280 kg/m3) (9.81 m/s2) (45 m)
= 3213756 N/m2(Pa)
= 3.2 MPa
The modulus of elasticity for the steel rod is 200 GPa (200 109 N/m2). The axial deformation at distance x = 45 m can be calculated with (4a)
dxx=45 = (7280 kg/m3) (9.81 m/s2) (45 m)2 / (2 (200 109 N/m2))
= 0.00036 m
= 0.4 mm
Related Topics
-
Beams and Columns
Deflection and stress in beams and columns, moment of inertia, section modulus and technical information. -
Mechanics
The relationships between forces, acceleration, displacement, vectors, motion, momentum, energy of objects and more.
Related Documents
-
American Standard Beams - S Beam
American Standard Beams ASTM A6 - Imperial units. -
American Wide Flange Beams
American Wide Flange Beams ASTM A6 in metric units. -
Area Moment of Inertia - Typical Cross Sections I
Typical cross sections and their Area Moment of Inertia. -
Beam Loads - Support Force Calculator
Calculate beam load and supporting forces. -
Beams - Fixed at Both Ends - Continuous and Point Loads
Stress, deflections and supporting loads. -
Beams - Fixed at One End and Supported at the Other - Continuous and Point Loads
Supporting loads, moments and deflections. -
Beams - Supported at Both Ends - Continuous and Point Loads
Supporting loads, stress and deflections. -
British Universal Columns and Beams
Properties of British Universal Steel Columns and Beams. -
Cantilever Beams - Moments and Deflections
Maximum reaction forces, deflections and moments - single and uniform loads. -
Euler's Column Formula
Calculate buckling of columns. -
HE-A Steel Beams
Properties of HE-A profiled steel beams. -
Normal Flange I-Beams
Properties of normal flange I profile steel beams. -
Threaded Rods - Loads in Imperial Units
Weight rating of threaded hanger rods. -
W Steel Beams - Allowable Uniform Loads
Allowable uniform loads. -
W-Beams - American Wide Flange Beams
Dimensions of American Wide Flange Beams ASTM A6 (or W-Beams) - Imperial units. -
Wood Beams - Strength of Material
Bending and compression strength of wood species used in beams. -
Young's Modulus, Tensile Strength and Yield Strength Values for some Materials
Young's Modulus (or Tensile Modulus alt. Modulus of Elasticity) and Ultimate Tensile Strength and Yield Strength for materials like steel, glass, wood and many more.




