Area Moment of Inertia with Definitions, Formulas & Calculator

Area Moment of Inertia or Moment of Inertia for an Area - also known as Second Moment of Area - I, is a property of shape that is used to predict deflection, bending and stress in beams.

Area Moment of Inertia - Imperial units

• inches⁴

Area Moment of Inertia - Metric units

• mm⁴
• cm⁴
• m⁴

Converting between Units

• 1 cm⁴ = 10^-8 m⁴ = 10⁴ mm⁴
• 1 in⁴ = 4.16×10⁵ mm⁴ = 41.6 cm⁴

Example - Convert between Area Moment of Inertia Units

9240 cm⁴ can be converted to mm⁴ by multiplying with 10⁴

(9240 cm⁴) 10⁴ = 9.24 10⁷ mm⁴

Area Moment of Inertia (Moment of Inertia for an Area or Second Moment of Area)

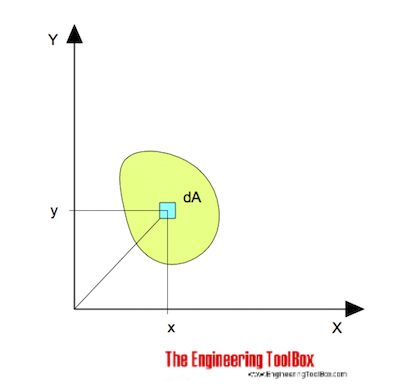
for bending around the x axis can be expressed as

I_x = ∫ y² dA                          (1)

where

I_x = Area Moment of Inertia related to the x axis (m⁴, mm⁴, inches⁴)

y = the perpendicular distance from axis x to the element dA (m, mm, inches)

dA = an elemental area (m², mm², inches²)

The Moment of Inertia for bending around the y axis can be expressed as

I_y = ∫ x² dA                          (2)

where

I_y = Area Moment of Inertia related to the y axis (m⁴, mm⁴, inches⁴)

x = the perpendicular distance from axis y to the element dA (m, mm, inches)

Area Moment of Inertia for typical Cross Sections I

• Area Moment of Inertia for typical Cross Sections II

Solid Square Cross Section

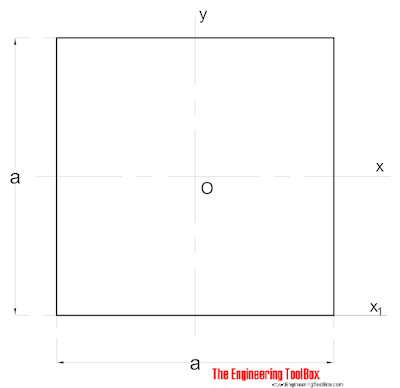
The Area Moment of Inertia for a solid square section can be calculated as

I_x = a⁴ / 12                        (2)

where

a = side (mm, m, in..)

 

I_y = a⁴ / 12                         (2b)

Solid Rectangular Cross Section

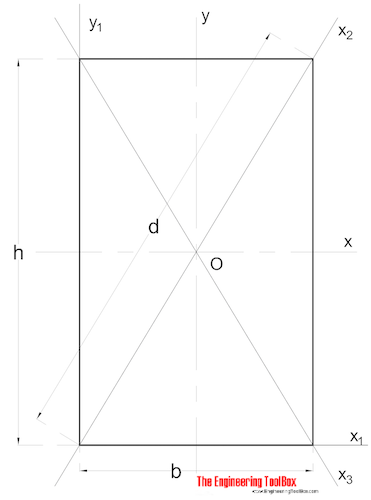
The Area Moment of Ineria for a rectangular section can be calculated as

I_x = b h³ / 12                          (3)

where

b = width

h = height

 

I_y = b³ h / 12                           (3b)

Solid Circular Cross Section

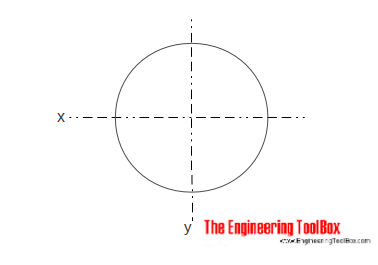
The Area Moment of Inertia for a solid cylindrical section can be calculated as

I_x = π r⁴ / 4

    = π d⁴ / 64                            (4)

where

r = radius

d = diameter

 

I_y = π r⁴ / 4

    = π d⁴ / 64                             (4b)

Hollow Cylindrical Cross Section

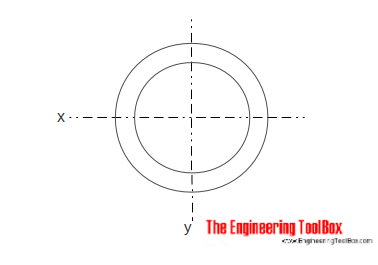
The Area Moment of Inertia for a hollow cylindrical section can be calculated as

I_x = π (d_o⁴ - d_i⁴) / 64                            (5)

where

d_o = cylinder outside diameter

d_i = cylinder inside diameter

 

I_y = π (d_o⁴ - d_i⁴) / 64                          (5b)

Square Section - Diagonal Moments

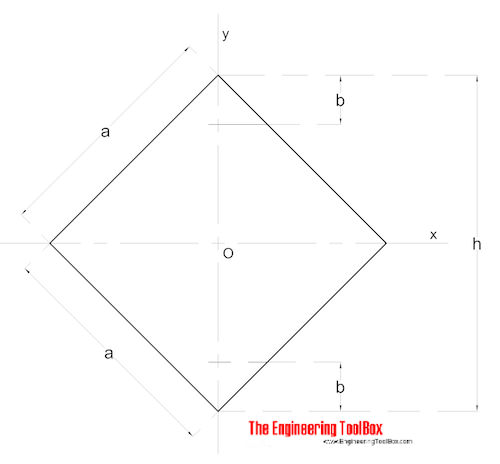
The diagonal Area Moments of Inertia for a square section can be calculated as

I_x = I_y = a⁴ / 12                   (6)

Rectangular Section - Area Moments on any line through Center of Gravity

Rectangular section and Area of Moment on line through Center of Gravity can be calculated as

I_x = (b h / 12) (h² cos²(a) + b² sin²(a))                  (7)

Symmetrical Shape

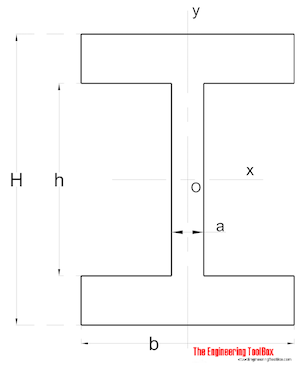
Area Moment of Inertia for a symmetrical shaped section can be calculated as

I_x = (a h³ / 12) + (b / 12) (H³ - h³)                       (8)

I_y = (a³ h / 12) + (b³ / 12) (H - h)                       (8b)

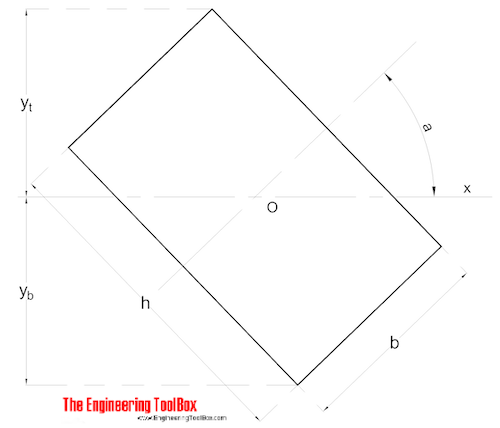
Nonsymmetrical Shape

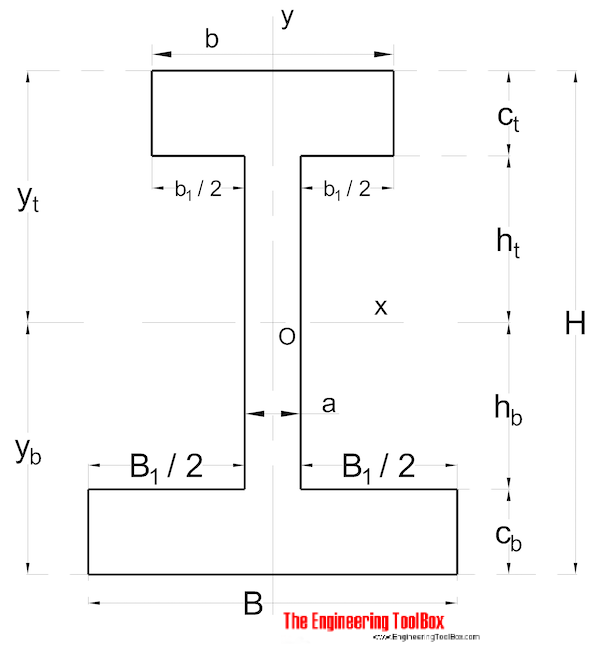
Area Moment of Inertia for a non symmetrical shaped section can be calculated as

I_x = 1/3 (B y_b³ - B₁ h_b³ + b y_t³ - b1 h_t³)                       (9)

• Area Moment of Inertia for typical Cross Sections II

Area Moment of Inertia vs. Polar Moment of Inertia vs. Moment of Inertia

• "Area Moment of Inertia" is a property of shape that is used to predict deflection, bending and stress in beams
• "Polar Moment of Inertia" as a measure of a beam's ability to resist torsion - which is required to calculate the twist of a beam subjected to torque
• "Moment of Inertia" is a measure of an object's resistance to change in rotation direction.

Section Modulus

• the "Section Modulus" is defined as W = I / y, where I is Area Moment of Inertia and y is the distance from the neutral axis to any given fiber