Stress
Stress is force applied on cross-sectional area.
Stress is the ratio between applied force and cross-sectional area where the applied force is acting.
Normal Stress
Normal stress can be expressed as
σ = FN / A (1)
where
σ = normal stress (N/m2, Pa, psi)
FN = applied force perpendicular to the area - Normal force (N, lb)
A = cross-sectional area (m2, in2)
Shear Stress
Shear stress can be expressed as
τ = FV / A (2)
where
τ = shear stress (N/m2, Pa, psi)
FV = applied force in plane of the area - Shear force (N, lb)
Example - Normal Stress in a Column
A 10000 N force is acting in the direction of a British Universal Column UB 152 x 89 x 16 with cross sectional area 20.3 cm2. The normal stress in the column can be calculated as
σ = (10000 N) / ((20.3 cm2) (0.0001 m2/cm2)
= 4926108 Pa (N/m2)
= 4.9 MPa
The Yield strength - the amount of stress that a material can undergo before moving from elastic deformation into plastic deformation - is typical 250 MPa for steel.
Example - Shear Stress in a Beam with Point Load
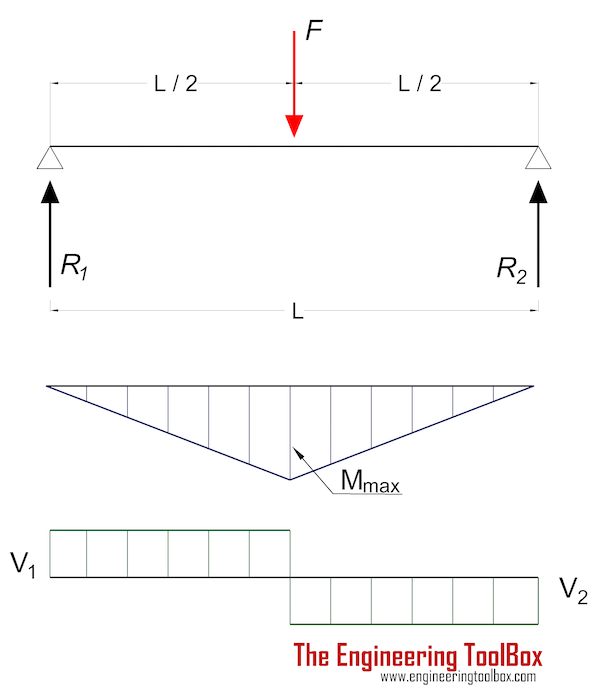
For a beam with single point load supported on both ends - the shear force Fv (or V in the figure above) is equal in magnitude to support force R1 or R2.
Reaction forces can be calculated due to moment equilibrium around support 1
F L / 2 = R2 L (4)
R2 = F / 2 (5)
R1 = R2 = F / 2 (6)
For a 10000 N point load perpendicular on a beam similar to the example above - supported at both ends - the magnitude of the reaction and shear forces can be calculated as
R1 = R2
= V1
= V2
= (10000 N) / 2
= 5000 N
= 5 kN
The shear stress can be calculated as
τ = (5000 N) / ((20.3 cm2) (0.0001 m2/cm2)
= 2463054 Pa
= 2.5 MPa
Related Topics
-
Mechanics
The relationships between forces, acceleration, displacement, vectors, motion, momentum, energy of objects and more. -
Statics
Forces acting on bodies at rest under equilibrium conditions - loads, forces and torque, beams and columns.
Related Documents
-
Beams - Fixed at Both Ends - Continuous and Point Loads
Stress, deflections and supporting loads. -
Beams - Fixed at One End and Supported at the Other - Continuous and Point Loads
Supporting loads, moments and deflections. -
Beams - Supported at Both Ends - Continuous and Point Loads
Supporting loads, stress and deflections. -
Process Pipes - Allowable Stress vs. Temperature
Allowable wall stress in pipes according ASME M31.3. -
Restricted Thermal Expansion - Force and Stress
Stress and force when thermal expansion a pipe, beam or similar is restricted. -
Rotating Bodies - Stress
Stress in rotating disc and ring bodies. -
Shafts Torsion
The torsion of solid or hollow shafts - Polar Moment of Inertia of Area. -
Steam Boiler Shells - Stress vs. Boiler Pressure
Calculate the stress in steam boiler shells caused by steam pressure. -
Steels - Endurance Limits and Fatigue Stress
Endurance limits and fatigue stress for steels. -
Stress in Thick-Walled Cylinders or Tubes
Radial and tangential stress in thick-walled cylinders or tubes with closed ends - with internal and external pressure. -
Stress in Thin-Walled Cylinders or Tubes
Hoop and longitudinal stress thin-walled tubes or cylinders. -
Stress, Strain and Young's Modulus
Stress is force per unit area - strain is the deformation of a solid due to stress. -
Threaded Bolts - Stress Area
Threaded bolts tensile stress area. -
Young's Modulus, Tensile Strength and Yield Strength Values for some Materials
Young's Modulus (or Tensile Modulus alt. Modulus of Elasticity) and Ultimate Tensile Strength and Yield Strength for materials like steel, glass, wood and many more.




