Euler Column Buckling: Formula, Theory & Calculator

Columns fail by buckling when their critical load is reached. Long columns can be analysed with the Euler column formula

F = n π² E I / L²                             (1) 

where

F = allowable load (lb, N)

n = factor accounting for the end conditions

E = modulus of elastisity (lb/in², Pa (N/m²))

L = length of column (in, m)

I = Moment of inertia (in⁴, m⁴)

Factor Counting for End Conditions

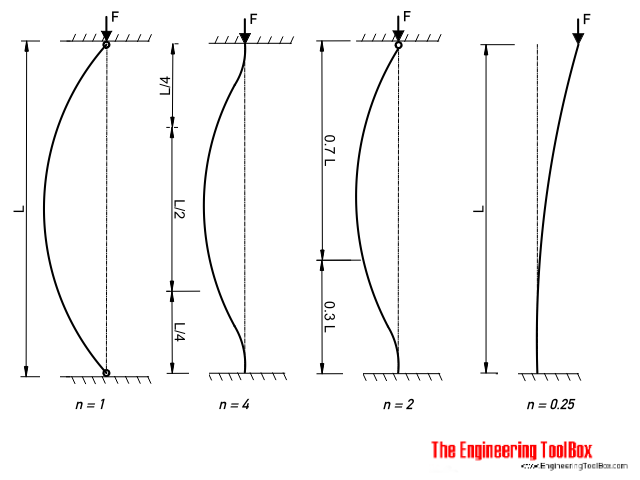
• column pivoted in both ends : n = 1
• both ends fixed : n = 4
• one end fixed, the other end rounded : n = 2
• one end fixed, one end free : n = 0.25

Note! 

Equation (1) is sometimes expressed with a k factor accounting for the end conditions:

F = π² E I / (k L)²                             (1b)

where

k = (1 / n)^1/2    factor accounting for the end conditions

n	1	4	2	0.25
k	1	0.5	0.7	2

Example - A Column Fixed in both Ends

An column with length 5 m is fixed in both ends. The column is made of an Aluminium I-beam 7 x 4 1/2 x 5.80 with a Moment of Inertia i_y = 5.78 in⁴. The Modulus of Elasticity of aluminum is 69 GPa (69×10⁹ Pa) and the factor for a column fixed in both ends is 4.

The Moment of Inertia can be converted to metric units like

I_y = 5.78 in⁴ (0.0254 m/in)⁴

    = 241×10^-8  m⁴

The Euler buckling load can then be calculated as

F = (4) π² (69×10⁹ Pa) (241×10^-8  m⁴) / (5 m)² 

 =  262594 N

 = 263 kN

Slenderness Ratio

The term "L/r" is known as the slenderness ratio. L is the length of the column and r is the radiation of gyration for the column.

• higher slenderness ratio - lower critical stress to cause buckling
• lower slenderness ratio - higher critical stress to cause buckling

• slenderness ratios L/r < 40: "short columns" where failure mode is crushing (yielding)
• slenderness ratios 40 < L/r < 120: "intermediate columns" where failure mode is a combination of crushing (yielding) and buckling
• slenderness ratio of 120 < L/r < 200: "long columns" where failure mode is buckling