Force
Newton's third law - force vs. mass and acceleration.
Force is an abstraction representing the push and pull interaction between objects.
The unit of force is the Newton (N) - where one newton is one kilogram metre per second squared . The Newton is defined as the force which, when applied to a mass of one kilogram , gives an acceleration of one meter per second squared .
F = m a (1)
where
F = force (N, lbf)
a = acceleration (m/s 2, ft/s2)
It is common to express forces as vectors with magnitude, direction and point of application. The net effect of two or more forces acting on the same point is the vector sum of the forces.
- 1 N = (1 kg) (1 m/s2)
- A Newton is the unbalanced force which will give a 1 kg mass an acceleration of 1 m/s2.
In the centimetre–gram–second system of units (cgs) - a variant of the metric system - the unit of force is called the dyne.
- 1 N = 100000 dyne
- A dyne is the unbalanced force which will give a 1 gram mass an acceleration of 1 cm/s2.
The unit of force in the Imperial or British system is the pound - lb, lbf .
- 1 lbf = 4.45 N
- A pound is the unbalanced force which will give a 1 slug mass an acceleration of 1 ft/s2.
Newton's Third Law
Newton's third law describes the forces acting on objects interacting with each other. Newton's third law can be expressed as
- "If one object exerts a force F on an other object, then the second object exerts an equal but opposite force F on the first object"
Body Force
A body force is when one body exerts a force on an other body without direct physical contact between the bodies. Examples - gravitation or electromagnetic fields.
Support Reactions
Surface forces at supports or points of contact between bodies are called reactions .
Acceleration
If there is a net unbalance between forces acting on a body the body accelerates. If the forces are balanced the body will not accelerate.
Example - Force and Acceleration
A mass of 50 kg is accelerated with 2 m/s2. The force required can be calculated as
F = (50 kg) (2 m/s2)
= 100 N
Example - Force due to Gravity (Weight)
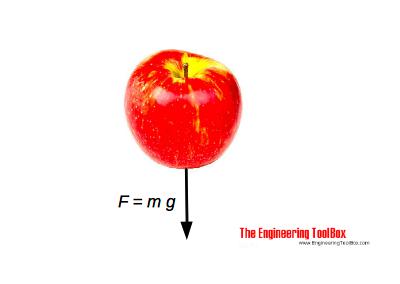
The gravity force - weight - on a apple with mass 50 g (0.050 kg) due to acceleration of gravity ag = 9.81 m/s2 - can be calculated as
F = (0.050 kg) (9.81 m/s2)
= 0.4905 N
Acceleration of Gravity on Earth
- SI units: ag = 9.81 m/s2
- Imperial units: ag = 32.174 ft/s2
- more about mass and weight
Force Calculator
The calculator below can used to calculate force due to mass and acceleration:
Example - Hoisting a Body
A body with mass m = 60 kg is hoisted by a winch. The force in the hoisting cable is Fc = 700 N. The gravity force weight - W - pulling the body downwards due to the gravity - can be calculated as
W = m ag
= (60 kg) (9.81 m/s2)
= 588.6 N
= 0.59 kN
The resulting acceleration force - Fa - which moves the body upwards - can be calculated by subtracting the weight of the body from the cable force as
Fa = (700 N) - (588.6 N)
= 111.4 N
= 0.11 kN
The acceleration of the body can be calculated as
a = Fa / m
= (111.4 N) / (60 kg)
= 1.86 m/s2