Impact Force
Impact forces acting on falling objects hitting the ground, cars crashing and similar cases.

The dynamic kinetic energy of a moving object, like a falling ball or a driving car, can be expressed as
E = 1/2 m v2(1)
where
E = kinetic (dynamic) energy (J, ft lb)
m = mass of the object (kg, slugs )
v = velocity of the object (m/s, ft/s)
In an impact - like a car crash - the work made by the impact force slowing down an moving object over a distance by deforming the crumple zone can be expressed as
W = F avg s (2)
where
W = work done (J, ft lb)
F avg = average impact force during deformation (N, lbf )
s = deformation distance, crumple zone (m, ft)
When a crumple zone deforms in a car crash the average impact force is designed to be as constant as possible.
In an impact where the object is not deformed - the work made by the impact force slowing down the moving object equals to the work done by a spring force - and can be expressed as
W = 1/2 F max s
= 1/2 k s2(2b)
where
W = work done (J, ft lb)
F max = maximum force at the end of the deformation (N, lbf )
k = spring constant
s = deformation distance (m, ft)
In a car crash the dynamic energy is converted to work and equation 1 and 2 can be combined to
F avg s = 1/2 m v2(3)
The average impact force can be calculated as
F avg = 1/2 m v2/ s (3b)
The deformation slow-down distance can be calculated as
s = 1/2 m v2/ F avg (3c)
Note! - The deformation slow-down distance is very important and the key to limit the forces acting on passengers in a car crash.
Example - Car Crash
A car with a mass of 2000 kg drives with speed 60 km/h (16.7 m/s) before it crashes into a massive concrete wall. The front of the car impacts 0.5 m (the deformation distance).
The impact force can be calculated as
F max = 1/2 (2000 kg) (16.7 m/s)2/ (0.5 m)
= 558 kN
Note that the gravitation force (weight) acting on the car is only
F w = m g
= (2000 kg) (9.81 m/s2)
= 19.6 kN
The impact creates a force 28 times gravity!!
A person sitting inside the car with seat belts on will de-accelerate with a force 28 times gravity . Note that the National Highway Traffic Safety Administration (NHTSA) states that "the maximum chest acceleration shall not exceed 60 times gravity for time periods longer than 3 milliseconds ". For a car crash with 90 km/h (25 m/s) the de-acceleration will be 64 times gravity (same parameters as above).
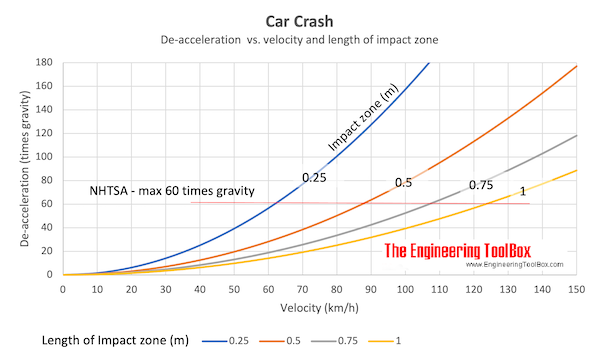
- 60 mph = 96.6 km/h
Impact Force from a Falling Object
The dynamic energy in a falling object at the impact moment when it hits the ground can be calculated as
E = F weight h
= m a g h (4)
where
F weight = force due to gravity - or weight (N, lbf )
a g = acceleration of gravity (9.81 m/s2, 32.17405 ft/s2)
h = falling height (m)
If the dynamic energy from the fall is converted to impact work - equation 2 and 4 can be combined to
F avg s = m a g h (5)
The impact force can be expressed as
F avg = m a g h / s (5b)
The deformation slow-down distance can be expressed as
s = m a g h / F avg (5c)
Example - a Falling Car
The same car as above falls from height 14.2 m and crashes on the crumple zone with the front down on a massive concrete tarmac. The front impacts 0.5 m (slow down distance) as above. The impact force can be calculated as
F avg = (2000 kg) (9.81 m/s2) (14.2 m) / (0.5 m)
= 558 kN
Note! - a car crash in 90 km/h (25 m/s) compares to a fall from 32 m !!
Example - a Person falling from a Table
A person with weight (gravitational force) of 200 lbs (lbf ) falls from a 4 feet high table.
The energy of the falling body when it hits the ground can be calculated using (4) as
E = (200 lbf ) (4 ft)
= 800 ft lb
The impact on a human body can be difficult to determine since it depends on how the body hits the ground - which part of the body, the angle of the body and/or if hands are used to protect the body and so on.
For this example we use an impact distance of 3/4 inch (0.0625 ft) to calculate the impact force:
F avg = (800 ft lb) / (0.0625 ft)
= 12800 lbf
In metric units - person with weight 90 kg, falling distance 1.2 m and impact distance 2 cm :
E = (90 kg) (9.81 m/s2) (1.2 m)
= 1059 J
F avg = (1059 J) / (0.02 m)
= 53 kN
Related Topics
-
Dynamics
Motion of bodies and the action of forces in producing or changing their motion - velocity and acceleration, forces and torque.
Related Documents
-
Bollard Forces
Friction, load and effort forces acting in ropes turned around bollards. -
Car - Required Power and Torque
Power, torque, efficiency and wheel force acting on a car. -
Car Acceleration
Car acceleration calculator. -
Car Fuel Consumption - liter/100 km
Calculate fuel consumption in liter per km - consumption chart and calculator. -
Cars - New vs. Old Car Cost Calculator
Calculate and compare the costs between owning a new vs. an old car. -
Conservation of Momentum
The momentum of a body is the product of its mass and velocity - recoil calculator. -
Driving Distances between European Cities
Driving distance between some major European cities. -
Force
Newton's third law - force vs. mass and acceleration. -
Fuel Consumption - mpg
Calculate fuel consumption in miles per gallon - mpg - calculator and consumption charts. -
Impulse and Impulse Force
Forces acting a very short time are called impulse forces. -
Jet Propulsion
Calculate the propulsive discharge force or thrust induced by an incompressible jet flow. -
Kinetic Energy
Energy possessed by an object's motion is kinetic energy. -
Piston Engines - Compression Ratios
Cylinder volume and compression ratios in piston engines. -
Piston Engines - Displacement
Calculate piston engine displacement. -
Rolling Resistance
Rolling friction and rolling resistance. -
Vehicle - Distance Traveled vs. Velcocity and Time Used (mph)
Speed (mph) and time (hours) and distance traveled (miles) chart. -
Vehicle - Distance Traveled vs. Velocity and Time (km/h)
Speed (km/h) vs. time (hours) and distance traveled (km). -
Work done by Force
Work done by a force acting on an object.




