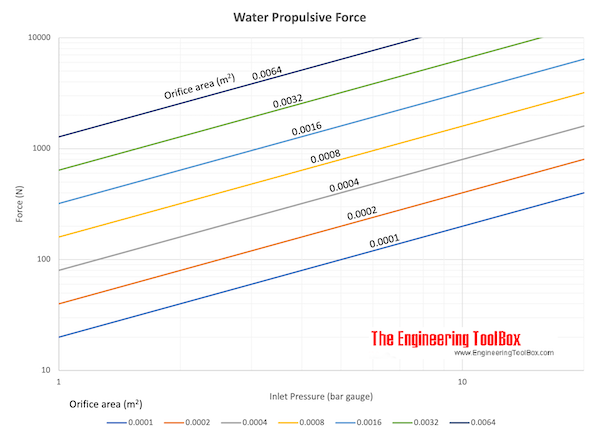
Jet Propulsion
Calculate the propulsive discharge force or thrust induced by an incompressible jet flow.
The velocity out of a free jet can be expressed as
v2 = (2 (p1 - p2) / ρ)1/2 (1)
where
v2 = velocity out of the jet (m/s)
p1 = pressure before the jet (N/m2, Pa)
p2 = ambient pressure after the jet (N/m2, Pa)
ρ = density of the fluid (kg/m3)
Note! - the density ρ is constant in incompressible flows and the equations are valid for liquids (like water) but not for gases (like air).
The flow volume out of a jet can be expressed as
q = A v2 (2)
where
q = volume flow (m3/s)
A = orifice area of the jet (m2)
The propulsive force or thrust induced by the jet can be expressed as
F = ρ q (v2- v1) (3)
where
v1 = jet velocity (m/s)
If the jet is not moving
v1 = 0
and (3) can be expressed as
F = ρ q v2 (3b)
- or alternatively with (2)
F = ρ A v22 (3c)
Substituting v2 with eq. (1) in eq. (3c) - the propulsive force or thrust induced by a jet not moving (v1 = 0) be expressed as
F = 2 A (p1 - p2) (4)
Example - Propulsive Force

Water flows through a garden hose with diameter 15 mm . The water pressure just before the outlet is 4×105 Pa (abs) and the atmospheric pressure is 1×105 Pa (abs).
The outlet area of the hose can be calculated as
A = π ((15 mm) (0.001 m/mm) / 2)2
= 1.77 10 -4 (m2)
The propulsive force can be calculated as
F = 2 ( 1.77×10-4 m2) (( 4×105 Pa) - ( 1×105 Pa))
= 106 N