Forces and Tensions in Ropes due to Angle
Reduced load capacities in ropes, cables or lines - due to acting angle.
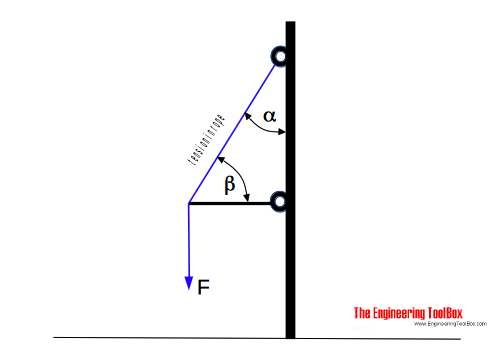
The increased force or tension in a rope or cable due to angles:
| Rope Angle with Load (degrees) | Increased Force or Tension Factor - θ - | |
|---|---|---|
| - α - | - β - | |
| 0 | 90 | 1.00 |
| 5 | 85 | 1.00 |
| 10 | 80 | 1.02 |
| 15 | 75 | 1.04 |
| 20 | 70 | 1.07 |
| 25 | 65 | 1.10 |
| 30 | 60 | 1.16 |
| 35 | 55 | 1.22 |
| 40 | 50 | 1.31 |
| 45 | 45 | 1.41 |
| 50 | 40 | 1.56 |
| 55 | 35 | 1.74 |
| 60 | 30 | 2.00 |
| 65 | 25 | 2.37 |
| 70 | 20 | 2.92 |
| 75 | 15 | 3.86 |
| 80 | 10 | 5.76 |
| 85 | 5 | 11.5 |
As we can see from the table above - with
α = 60 degrees
and
β = 30 degrees
the force or tension F in the rope is doubled.
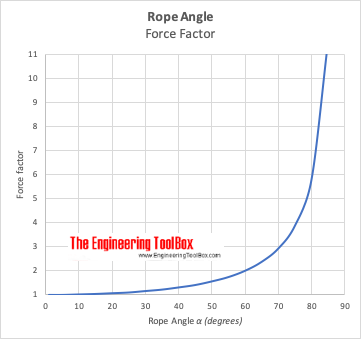
The force acting in the rope can be calculated as
Frope = θ F (1)
where
Frope = force acting in the rope (N, lb)
θ = increased force or tension factor from the table above
F = load (N, lb)
The force acting in the horizontal beam can be calculated as
Fbeam = (Frope2 + F2)1/2 (2)
The angle α can be calculated as
α = tan-1(h / d) (3)
where
α = angle (degrees)
h = vertical distance between horizontal beam and rope (m, ft)
d = length of horizontal beam (m, ft)
The angle β can be calculated as
β = tan-1(d / h) (4)
where
β = angle (degrees)
Example - Increased Force in a Rope due to Angle
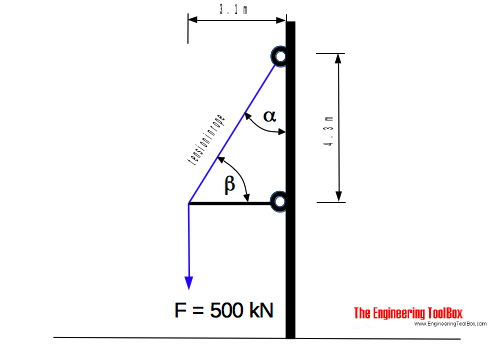
The maximum force in the rope in the figure above can be estimated by firs calculate the angles:
α = tan-1(3.1 / 4.3)
= 35.8o
β = tan-1(4.3 / 3.1)
= 54.2o
From the table above the tension factor is approximately 1.22 and the force in the rope can be calculated as
Frope = (500 kN) 1.22
= 610 kN



