Liquids - Densities vs. Pressure and Temperature Change
Densities and specific volume of liquids vs. pressure and temperature change.
The density of a liquid will change with temperature and pressure. The density of water versus temperature and pressure is indicated below:
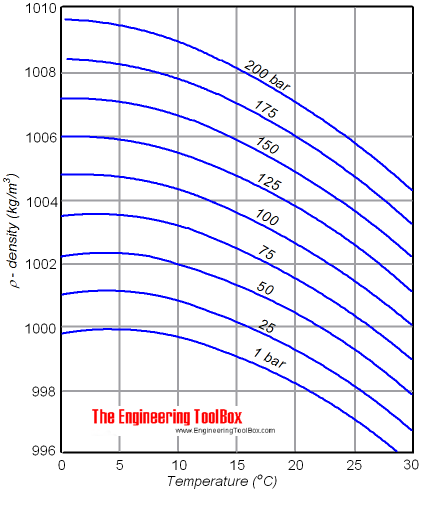
See also Water - Density, Specific Weight and Thermal Expantion Coefficient, for online calculator, figures and tables showing changes with temperature.
Density
The density of a liquid can be expressed as
ρ = m / V (1)
where
ρ = density of liquid (kg/m3)
m = mass of the liquid (kg)
V = volume of the liquid (m3)
The inverse of density is specific volume:
v = 1 / ρ
= V / m (2)
where
v = specific volume (m3/kg)
Volume and change in Temperature
When temperature increases - most liquids expands:
dV = V1 - V0
= V0 β dt
= V0 β (t1 - t0) (3)
where
dV = V1 - V0 = change in volume - difference between final and initial volume (m3)
β = volumetric temperature expansion coefficient (m3/m3 o C)
dt = t1 - t0 = change in temperature - difference between final and initial temperature (oC)
(3) can be modified to
V1 = V0 (1 + β (t1 - t0)) (3b)
Density and change in Temperature
With (1) and (3b) the final density after a temperature change can be expressed as
ρ1 = m / (V0 (1 + β (t1 - t0))) (4)
where
ρ1 = final density (kg/m3)
- or combined with (2)
ρ1 = ρ0 / (1 + β (t1 - t0)) (4b)
where
ρ0 = initial density (kg/m3)
Volumetric Temperature Coefficients - β
- water : 0.0002 (m3/m3 oC) at 20 oC
- ethyl alcohol : 0.0011 (m3/m3 oC)
- volumetric expansion coefficient for some commonly used materials
Note! - volumetric temperature coefficients may vary strongly with temperature.
Density and change in Pressure
The influence of pressure on the volume of a liquid can be expressed with the three dimensional Hooke's law
E = - dp / (dV / V0)
= - (p1 - p0) / ((V1 - V0) / V0) (5)
where
E = bulk modulus - liquid elasticity (N/m2)
The minus sign corresponds to the fact that an increase in the pressure leads to a decrease in volume.
With (5) - the final volume after pressure change can be expressed as
V1 = V0 (1 - (p1 - p0) / E) (5b)
Combining (5b) with (1) - the final density can be expressed as:
ρ1 = m / (V0 (1 - (p1 - p0) / E)) (6)
- or combined with (2) - the final density can be expressed as
ρ1 = ρ0/ (1 - (p1 - p0) / E) (6b)
Bulk Modulus Fluid Elasticity some common Fluids - E
- water : 2.15×109 (N/m2)
- ethyl alcohol : 1.06×109 (N/m2)
- oil : 1.5×109 (N/m2)
Note! Bulk modulus for liquids varies with pressure and temperature.
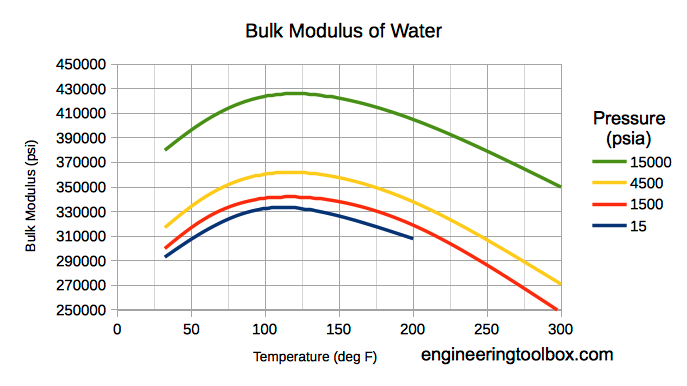
Bulk modulus for water - Imperial Units
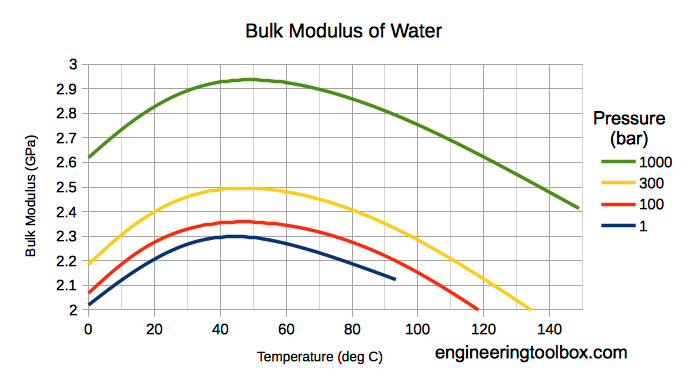
Bulk modulus for Water - SI units
Density of a fluid changing both Temperature and Pressure
The density of a fluid when changing both temperature and pressure can be expressed combining (4b) and (6b) :
ρ1 = ρ1(from eq.1) / (1 - (p1 - p0) / E)
= ρ0 / (1 + β (t1 - t0)) / (1 - (p1 - p0) / E) (7)
Example - Density of Water at 100 bar and 20 oC
- density of water 0 oC : 999.8 (kg/m3)
- expansion coefficient of water at 10 oC : 0.000088 ( m3/m3 oC) (average value between 0 and 20 oC)
- bulk modulus of water: 2.15×109 (N/m2)
Density of water can be calculated with (3):
ρ1 = (999.8 kg/m3) / (1 + (0.000088 m3/m3 oC) ((20 oC) - (0 oC))) / (1 - ((100×105 Pa) - (1×105 Pa)) / ( 2.15×109 N/m2))
= 1002.7 (kg/m3)



