Bulk Modulus and Fluid Elasticities
Introduction to - and definition of - Bulk Modulus Elasticity commonly used to characterize the compressibility of fluids.
The Bulk Modulus Elasticity - or Volume Modulus - is a material property characterizing the compressibility of a fluid - how easy a unit volume of a fluid can be changed when changing the pressure working upon it.
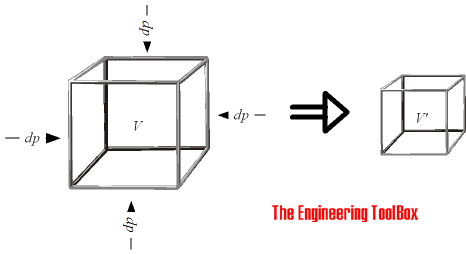
The Bulk Modulus Elasticity can be calculated as
K = - dp / (dV / V0 )
= - ( p1 - p0 ) / ((V1 - V0 ) / V0 ) (1)
where
K = Bulk Modulus of Elasticity (Pa, N/m2)
dp = differential change in pressure on the object (Pa, N/m2)
dV = differential change in volume of the object (m3 )
V0 = initial volume of the object (m3 )
p0 = initial pressure ( Pa, N/m2)
p1 = final pressure ( Pa, N/m2)
V1 = final volume ( m3 )
The Bulk Modulus Elasticity can alternatively be expressed as
K = dp / (dρ / ρ0 )
= ( p1 - p0 ) / (( ρ1 - ρ0 ) / ρ0 ) (2)
where
dρ = differential change in density of the object (kg/m3 )
ρ0 = initial density of the object (kg/m3 )
ρ1 = final density of the object ( kg/m3 ) <
An increase in the pressure will decrease the volume (1). A decrease in the volume will increase the density (2) .
- The SI unit of the bulk modulus elasticity is N/m2(Pa)
- The imperial (BG) unit is lbf /in2(psi)
- 1 lbf /in2(psi) = 6.894 103 N/m2(Pa)
A large Bulk Modulus indicates a relative incompressible fluid.
Bulk Modulus Common Fluids
| Fluid | Bulk Modulus - K - | |
|---|---|---|
| Imperial Units - BG ( 105 psi, lbf /in2) | SI Units ( 109 Pa, N/m2) | |
| Acetone | 1.34 | 0.92 |
| Benzene | 1.5 | 1.05 |
| Carbon Tetrachloride | 1.91 | 1.32 |
| Ethyl Alcohol | 1.54 | 1.06 |
| Gasoline | 1.9 | 1.3 |
| Glycerin | 6.31 | 4.35 |
| ISO 32 mineral oil | 2.6 | 1.8 |
| Kerosene | 1.9 | 1.3 |
| Mercury | 41.4 | 28.5 |
| Paraffin Oil | 2.41 | 1.66 |
| Petrol | 1.55 - 2.16 | 1.07 - 1.49 |
| Phosphate ester | 4.4 | 3 |
| SAE 30 Oil | 2.2 | 1.5 |
| Seawater | 3.39 | 2.34 |
| Sulfuric Acid | 4.3 | 3.0 |
| Water (10 oC) | 3.12 | 2.09 |
| Water - glycol | 5 | 3.4 |
| Water in oil emulsion | 3.3 | 2.3 |
- 1 GPa = 109 Pa (N/m2)
Stainless steel with Bulk Modulus 163 109 Pa is aprox. 80 times harder to compress than water with Bulk Modulus 2.15 109 Pa .
Example - Density of Seawater in the Mariana Trench
- the deepest known point in the Earth's oceans - 10994 m .
The hydrostatic pressure in the Mariana Trench can be calculated as
p1 = (1022 kg/m3 ) (9.81 m/s2) (10994 m)
= 110 106 Pa (110 MPa)
The initial pressure at sea-level is 105 Pa and the density of seawater at sea level is 1022 kg/m3 .
The density of seawater in the deep can be calculated by modifying (2) to
ρ1 = ( ( p1 - p0 ) ρ0 + K ρ0 ) / K
= (((110 106 Pa) - (1 105 Pa)) (1022 kg/m3 ) + (2.34 109 Pa) (1022 kg/m3 )) / ( 2.34 109 Pa )
= 1070 kg/m3
Note! - since the density of the seawater varies with dept the pressure calculation could be done more accurate by calculating in dept intervals.
Bulk Modulus of Water vs. Temperature
| Temperature (oC) | Bulk Modulus (109 Pa) |
|---|---|
| 0.01 | 1.96 |
| 10 | 2.09 |
| 20 | 2.18 |
| 30 | 2.23 |
| 40 | 2.26 |
| 50 | 2.26 |
| 60 | 2.25 |
| 70 | 2.21 |
| 80 | 2.17 |
| 90 | 2.11 |
| 100 | 2.04 |
Related Topics
-
Fluid Mechanics
The study of fluids - liquids and gases. Involving velocity, pressure, density and temperature as functions of space and time. -
Material Properties
Properties of gases, fluids and solids. Densities, specific heats, viscosities and more.
Related Documents
-
Cauchy Number
Introduction to the Cauchy Number. -
Heavy Water - Thermophysical Properties
Thermodynamic properties of heavy water (D2O) like density, melting temperature, boiling temperature, latent heat of fusion, latent heat of evaporation, critical temperature and more. -
Liquids - Densities vs. Pressure and Temperature Change
Densities and specific volume of liquids vs. pressure and temperature change. -
Mach Number
An introduction to the Mach Number. -
Metals and Alloys - Bulk Modulus Elasticity
The Bulk Modulus - resistance to uniform compression - for some common metals and alloys. -
Minerals - Densities
Densities of minerals. -
Modulus of Rigidity
Shear Modulus (Modulus of Rigidity) is the elasticity coefficient for shearing or torsion force. -
Speed of Sound - Equations
Calculate the speed of sound (the sonic velocity) in gases, fluids or solids. -
Water Hammer
Rapidly closing or opening valves - or starting stopping pumps - may cause pressure transients in pipelines known as surge or water hammers.




