Cooling and Heating Equations

Sensible Heat

The sensible heat in a heating or cooling process of air (heating or cooling capacity) can be calculated in SI-units as

h _s = c _p ρ q dt (1)

where

h _s = sensible heat (kW)

c _p = specific heat of air (1.006 kJ/kg ^o C)

ρ = density of air (1.202 kg/m ³ )

q = air volume flow (m ³ /s)

dt = temperature difference ( ^o C)

Or in Imperial units as

h _s = 1.08 q dt (1b)

where

h _s = sensible heat (Btu/hr)

q = air volume flow (cfm, cubic feet per minute)

dt = temperature difference ( ^o F)

Example - Heating Air, Sensible Heat

Metric Units

An air flow of 1 m ³ /s is heated from 0 to 20 ^o C . Using (1) the sensible heat added to the air can be calculated as

h _s = (1.006 kJ/kg ^o C) (1.202 kg/m ³ ) ( 1 m ³ /s ) ((20 ^o C) - (0 ^o C))

= 24.2 (kW)

Imperial Units

An air flow of 1 cfm is heated from 32 to 52 ^o F . Using (1b) the sensible heat added to the air can be calculated as

h _s = 1.08 (1 cfm) ((52 ^o F) - (32 ^o F))

= 21.6 (Btu/hr)

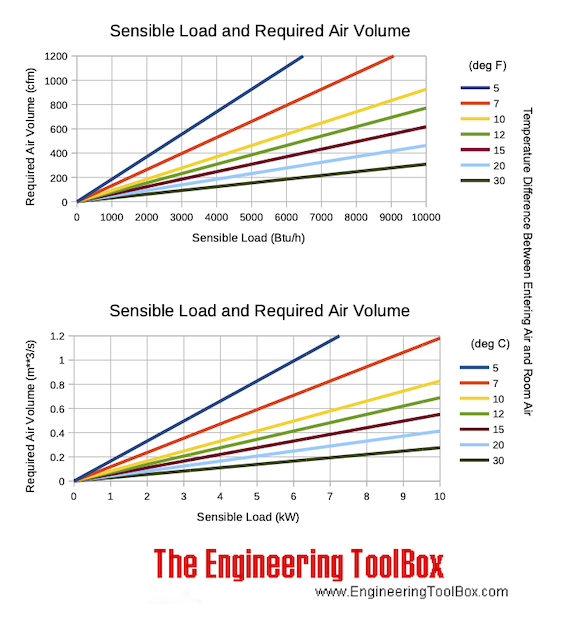
Sensible Heat Load and Required Air Volume Chart

Sensible heat load and required air volume to keep the temperature constant at various temperature differences between make up air and room air:

• Sensible Heat Load and Required Air Volume Chart (pdf)

Latent Heat

Latent heat due to the moisture in air can be calculated in SI-units as:

h _l = ρ h _we q dw _kg (2)

where

h _l = latent heat (kW)

ρ = density of air (1.202 kg/m ³ )

q = air volume flow (m ³ /s)

h _we = latent heat evaporization water ( 2454 kJ/kg - in air at atmospheric pressure and 20 ^o C)

dw _kg = humidity ratio difference (kg water/kg dry air)

• estimate humidity with the Mollier diagram

Latent evaporation heat for water can be calculated as

h _we = 2494 - 2.2 t                  (2a)

where

t = evaporation temperature ( ^o C)

Or for Imperial units:

h _l = 0.68 q dw _gr (2b)

or

h _l = 4840 q dw _lb (2c)

where

h _l = latent heat (Btu/hr)

q = air volume flow (cfm, cubic feet per minute)

dw _gr = humidity ratio difference (grains water/lb dry air)

dw _lb = humidity ratio difference (lb water/lb dry air)

• 1 grain = 0.000143 lb = 0.0648 g

• Psychrometric chart

Example - Cooling Air, Latent Heat

Metric Units

An air flow of 1 m ³ /s is cooled from 30 to 10 ^o C . The relative humidity of the air is 70% at the start and 100% at the end of the cooling process.

From the Mollier diagram we estimate the water content in the hot air to be 0.0187 kg water/kg dry air, and the water content in the cold air to be 0.0075 kg water/kg dry air .

Using (2) the latent heat removed from the air can be calculated as

h _l = (1.202 kg/m ³ ) ( 2454 kJ/kg ) ( 1 m ³ /s ) (( 0.0187 kg water/kg dry air ) - ( 0.0075 kg water/kg dry air ))

= 34.3 (kW)

Imperial Units

An air flow of 1 cfm is cooled from 52 to 32 ^o F . The relative humidity of the air is 70% at the start and 100% at the end of the cooling process.

From the psychrometric chart we estimate the water content in the hot air to be 40 grains water/lb dry air , and the water content in the cold air to be 26 grains water/lb dry air .

Using (2b) the latent heat removed from the air can be calculated as

h _l = 0.68 (1 cfm) (( 40 grains water/lb dry air ) - ( 26 grains water/lb dry air ))

= 9.5 (Btu/hr)

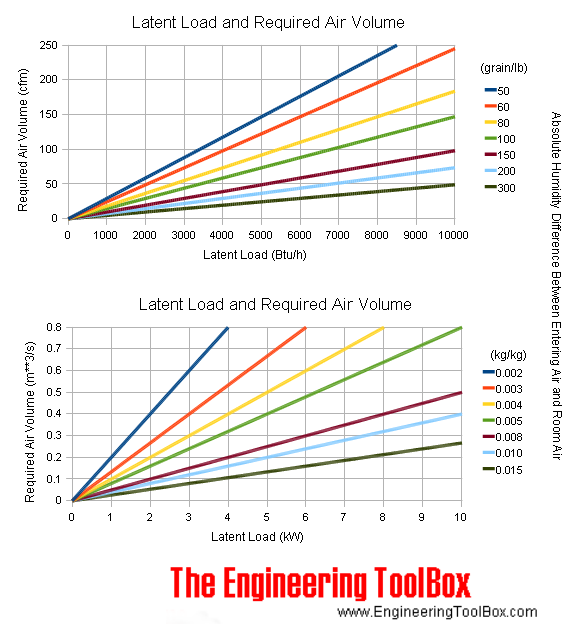
Latent Heat Load and Required Air Volume Chart

Latent heat load - humidifying and dehumidifying - and required air volume to keep temperature constant at various temperature differences between entering air and room air are indicated in the chart below:

• Latent Heat Load and Required Air Volume Chart (pdf)

Total Heat - Latent and Sensible Heat

Total heat due to both temperature and moisture can be expressed in SI units as:

h _t = ρ q dh                                            (3)

where

h _t = total heat (kW)

q = air volume flow (m ³ /s)

ρ = density of air (1.202 kg/m ³ )

dh = enthalpy difference (kJ/kg)

• estimate enthalpy with the Mollier diagram

Or - in imperial units:

h _t = 4.7 q dh (3b)

where

h _t = total heat (Btu/hr)

q = air volume flow (cfm, cubic feet per minute)

dh = enthalpy difference (btu/lb dry air)

Total heat can also be expressed as:

h _t = h _s + h _l

= 1.08 q dt + 0.68 q dw _gr (4)

Example - Cooling or Heating Air, Total Heat

Metric Units

An air flow of 1 m ³ /s is cooled from 30 to 10 ^o C . The relative humidity of the air is 70% at the start and 100% at the end of the cooling process.

From the Mollier diagram we estimate the water enthalpy in the hot air to be 77 kJ/kg dry air, and the enthalpy in the cold air to be 28 kJ/kg dry air .

Using (3) the total sensible and latent heat removed from the air can be calculated as

h _t = (1.202 kg/m ³ ) ( 1 m ³ /s ) (( 77 kJ/kg dry air ) - (28 kJ/kg dry air ))

= 58.9 (kW)

Imperial Units

An air flow of 1 cfm is cooled from 52 to 32 ^o F . The relative humidity of the air is 70% at the start and 100% at the end of the cooling process.

From the psychrometric chart we estimate the water enthalpy in the hot air to be 18.7 Btu /lb dry air , and the enthalpy in the cold air to be 11.8 Btu /lb dry air .

Using (3b) the total sensible and latent heat removed from the air can be calculated as

h _t = 4.7 (1 cfm) (( 18.7 Btu /lb dry air ) - ( 11.8 Btu /lb dry air ))

= 32.4 (Btu/hr)

SHR - Sensible Heat Ratio

The Sensible Heat Ratio can be expressed as

SHR = h _s / h _t (6)

where

SHR = Sensible Heat Ratio

h _s = sensible heat

h _t = total heat (sensible and latent)

Temperature ^oC
K
^oF

Length m
km
in
ft
yards
miles
naut miles

Area m²
km²
in²
ft²
miles²
acres

Volume m³
liters
in³
ft³
us gal

Weight kg_f
N
lbf

Velocity m/s
km/h
ft/min
ft/s
mph
knots

Pressure Pa
bar
mm H₂O
kg/cm²
psi
inches H₂O

Flow m³/s
m³/h
US gpm
cfm