Electric Heating of Mass
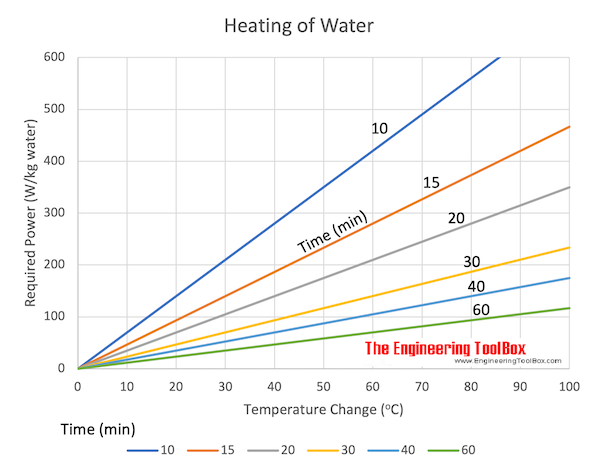
Electric heating of an object or mass - temperature change vs. energy supplied.
When an electric heater heats an object - the electric energy is transformed to heat by increased object temperature. The electric energy used equals the change in thermal energy and can be expressed as:
P t μ = U I t μ
= c m dT (1)
electric energy supplied = thermal energy change in object
where
P = power (watts, W)
U = potential difference (volts, V)
I = electrical current (amps, A)
t = time (sec)
μ = heating efficiency
c = specific heat of the heated substance (J/kgoC)
m = mass of the heated substance (kg)
dT = temperature differance (oC)
Example - 12 Volt Car Water Heater
The temperature change in a 12 volts and 10 amps Car Water Heater (100% efficient => μ = 1) with 0.4 kg water and 5 minutes heating period can be calculated by modifying (1) to
dT = U I t μ / c m
= (12 volts) (10 amps) (300 sec) 1 / (4200 J/kgoC) (0.4 kg)
= 21.4 oC
Note! The mass of the water heater and the heat loss from the heater during heating is neglected in the calculation. In reality the mass of the heater and the heat loss from the heater during the heating process will influence the temperature change.
Electric Heating Calculator
This calculator can be used to calculate temperature rise in an electric heated object or mass. Heat loss during heating is neglected.
Related Topics
-
Electrical
Electrical engineering with units, amps and electrical wiring. Wire gauges, electrical formulas, motors and more. -
Thermodynamics
Calculate heat, work, temperature and energy. The thermodynamics of steam and condensate systems. Water and Ice properties.
Related Documents
-
Cooling and Heating Equations
Latent and sensible cooling and heating equations - imperial units. -
Heat, Work and Energy
Heat vs. work vs. energy. -
Heating Up Applications - Energy Required and Heat Transfer Rates
Energy required to heat up a substance. -
Liquids and Fluids - Specific Heats
Specific heats for some common liquids and fluids - acetone, oil, paraffin, water and many more. -
Solids - Specific Heats
Common solids - like brick, cement, glass and many more - and their specific heats - in Imperial and SI units. -
Specific Heat of common Substances
Specific heat of products like wet mud, granite, sandy clay, quartz sand and more. -
Storing Thermal Heat in Materials
Energy stored as sensible heat in materials. -
Units of Heat - BTU, Calorie and Joule
The most common units of heat BTU - British Thermal Unit, Calorie and Joule. -
Water - Thermophysical Properties
Thermal properties of water at different temperatures like density, freezing temperature, boiling temperature, latent heat of melting, latent heat of evaporation, critical temperature and more.
