Arithmetic and Logarithmic Mean Temperature Difference

According to Newton's Law of Cooling heat transfer rate is related to the instantaneous temperature difference between hot and cold media

• in a heat transfer process the temperature difference vary with position and time

Mean Temperature Difference

The mean temperature difference in a heat transfer process depends on the direction of fluid flows involved in the process. The primary and secondary fluid in an heat exchanger process may

• flow in the same direction - parallel flow or co-current flow
• in the opposite direction - counter-current flow
• or perpendicular to each other - cross flow

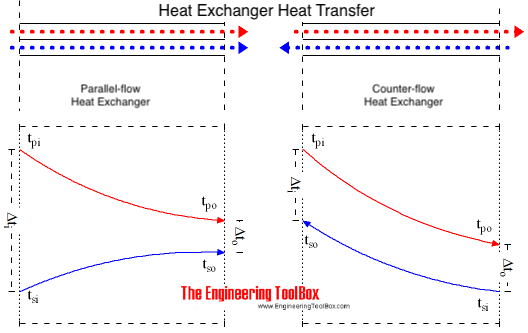
With saturation steam as the primary fluid the primary temperature can be taken as a constant since the heat is transferred as a result of a change of phase only. The temperature profile in the primary fluid is not dependent on the direction of flow.

Logarithmic Mean Temperature Difference - LMTD

The rise in secondary temperature is non-linear and can best be represented by a logarithmic calculation. A logarithmic mean temperature difference is termed

• LMTD (or DT_LM) - Logarithmic Mean Temperature Difference

LMTD can be expressed as

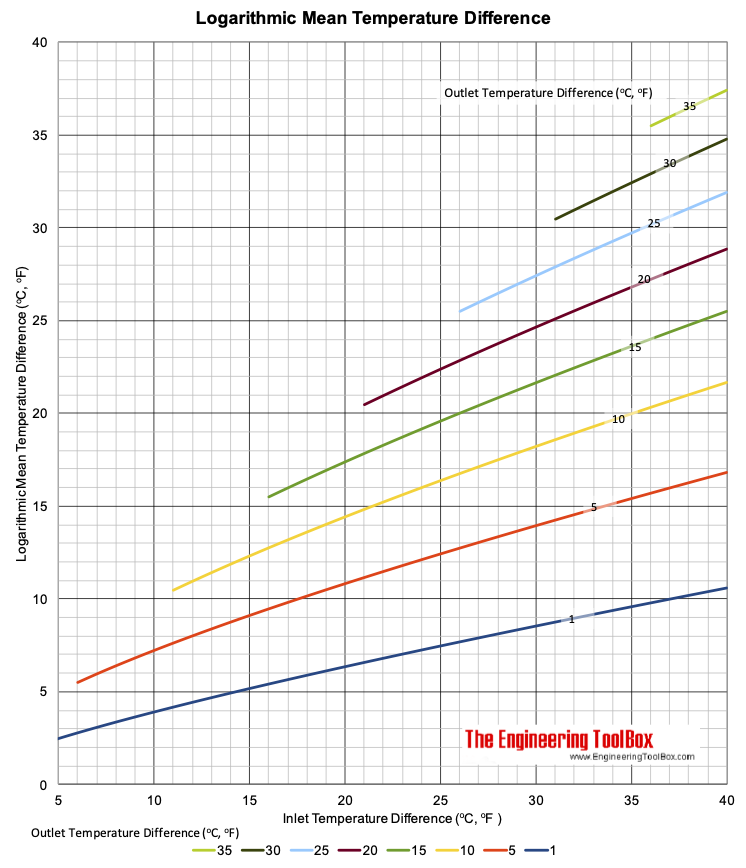
LMTD = (dt_i - dt_o) / ln(dt_i / dt_o)                                       (1)

where

LMTD = Logarithmic Mean Temperature Difference (^oF, ^oC)

For parallel flow:

dt_i = t_pi - t_si = inlet primary and secondary fluid temperature difference (^oF, ^oC)

dt_o = t_po - t_so = outlet primary and secondary fluid temperature difference (^oF, ^oC)

For counter flow:

dt_i = t_pi - t_so = inlet primary and outlet secondary fluid temperature difference (^oF, ^oC)

dt_o = t_po - t_si = outlet primary and inlet secondary fluid temperature difference (^oF, ^oC)

The Logarithmic Mean Temperature Difference is always less than the Arithmetic Mean Temperature Difference.

Arithmetic Mean Temperature Difference - AMTD

An easier but less accurate way to calculate the mean temperature difference is the

• AMTD (or DT_AM) - Arithmetic Mean Temperature Difference

AMTD can be expressed as:

AMTD = (t_pi + t_po) / 2 - (t_si + t_so) / 2                                  (2)

where

AMTD = Arithmetic Mean Temperature Difference (^oF, ^oC)

t_pi = primary inlet temperature (^oF, ^oC)

t_po = primary outlet temperature (^oF, ^oC)

t_si = secondary inlet temperature (^oF, ^oC)

t_so = secondary outlet temperature (^oF, ^oC)

A linear increase in the secondary fluid temperature makes it more easy to do manual calculations. AMTD will in general give a satisfactory approximation for the mean temperature difference when the smallest of the inlet or outlet temperature differences is more than half the greatest of  the inlet or outlet temperature differences.

When heat is transferred as a result of a change of phase like condensation or evaporation the temperature of the primary or secondary fluid remains constant. The equations can then be simplified by setting

t_p1 = t_p2

or

t_s1 = t_s2

Arithmetic and Logarithmic Mean Temperature Difference Calculator

The calculator below can be used to calculate Arithmetic and Logarithmic Mean Temperature Difference of counter-flow an parallel-flow heat exchangers.

Logarithmic Mean Temperature Difference Chart

• Logarithmic Mean Temperature Difference Chart (pdf)

Example - Arithmetic and Logarithmic Mean Temperature, Hot Water Heating Air

Hot water at 80 ^oC heats air from from a temperature of 0 ^oC to 20 ^oC in a parallel flow heat exchanger. The water leaves the heat exchanger at 60 ^oC.

Arithmetic Mean Temperature Difference can be calculated as

AMTD = ((80 ^oC) + (60 ^oC)) / 2 - ((0 ^oC) + (20 ^oC)) / 2

    = 60 ^oC

Logarithmic Mean Temperature Difference can be calculated as

LMTD = ((60 ^oC) - (20 ^oC)) - ((80 ^oC) - (0 ^oC))) / ln(((60 ^oC) - (20 ^oC)) / ((80 ^oC) - (0 ^oC)))

    = 57.7 ^oC

Example - Arithmetic and Logarithmic Mean Temperature, Steam Heating Water

Steam at 2 bar gauge heats water from 20 ^oC to 50 ^oC. The saturation temperature of steam at 2 bar gauge is 134 ^oC.

Note! that steam condenses at a constant temperature. The temperature on the heat exchangers surface on the steam side is constant and determined by the steam pressure.

• Steam Table

Arithmetic Mean Temperature Difference can be calculated like

AMTD = ((134 ^oC) + (134 ^oC)) / 2 - ((20 ^oC) + (50 ^oC)) / 2

    = 99 ^oC

Log Mean Temperature Difference can be calculated like

LMTD = ((134 ^oC) - (20 ^oC) - ((134 ^oC) - (50 ^oC))) / ln(((134 ^oC) - (20 ^oC)) / ((134 ^oC) - (50 ^oC)))

    = 98.24 ^oC