Humid Air - Heating
Enthalpy change and temperature rise when heating humid air without adding moisture.
The process of sensible heating of air - heating without adding moisture - can be visualized in the Mollier diagram as:
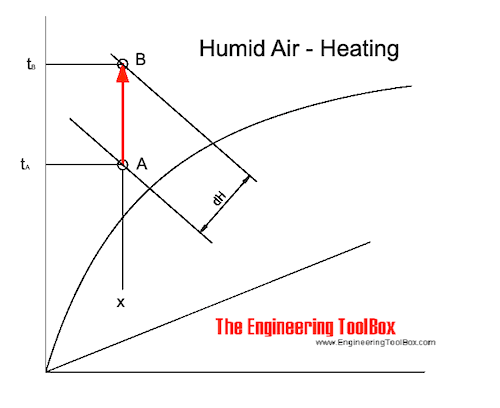
Sensible heating of air changes the state of the air from A to B along the constant specific humidity - x - line. The supplied heat - dH - can be estimated as indicated in the diagram above.
The heating process can also be visualized in the psychrometric chart
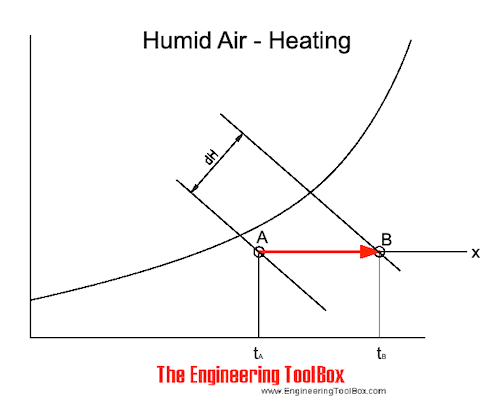
Note! - when sensible heating of air - the specific moisture remains constant - the relative humidity is decreased.
Calculating Enthalpy
The enthalpy of moist air can be calculated as:
h = cpa t + x (cpw t + hwe) (1)
where
h = specific enthalpy of moist air (kJ/kg)
cpa = 1.01 - specific heat capacity of air at constant pressure (kJ/kg oC, kWs/kgK)
t = air temperature (oC)
x = humidity ratio (kg/kg)
cpw = 1.84 - specific heat capacity of water vapor at constant pressure (kJ/kg. oC, kWs/kg.K)
hwe = 2502 - evaporation heat of water at 0 oC (kJ/kg)
(1) can be modified to:
h = 1.01 (kJ/kg. oC) t + x (1.84 (kJ/kg. oC) t + 2502 (kJ/kg)) (1b)
The Enthalpy Difference
The enthalpy difference when heating air without adding moisture can be calculated as:
dhA-B = cpa tB + x (cpw tB + hwe ) - cpa tA + x (cpw tA + hwe )
= cpa (tB - tA ) + x cpw (tB - tA ) (2)
Example - Enthalpy Change when Heating Air
The specific humidity of air at 25 oC and relative moisture 50% is 0.0115 kg/kg - check the Mollier diagram . The change in enthalpy when heating the air to 35 oC can be calculated as:
dhA-B = (1.01 kJ/kg oC)(35 oC - 25 oC) + (0.0115 kg/kg) (1.84 kJ/kg oC) (35 oC - 25 oC)
= (10.1 kJ/kg) + (0.2 kJ/kg)
= 10.3 (kJ/kg)
Note! - the contribution from the water vapor is relatively small and can for practical purposes often be neglected. (2) can then be modified to:
dhA-B = cpa ( tB - tA ) (2b)
Increase in Temperature when Heating Air
If heat is added to humid air the increase in air temperature can be calculated by modifying (2b) to:
tB - tA = dhA-B / cpa (2c)
Example - Heating Air and Temperature Rise
If 10.1 kJ is added to 1 kg air the temperature rise can be calculated as:
tB - tA = (10.1 kJ/kg) / (1.01 kJ/kg oC)
= 10 (oC)
Heat Flow in a Heating Coil
The total heat flow rate through a heating coil can be calculated as:
q = m (hB - hA ) (3)
where
q = heat flow rate (kJ/s, kW)
m = mass flow rate of air (kg/s)
The total heat flow can also be expressed as:
qs = L ρ (hB - hA ) (3a)
where
L = air flow rate (m3/s)
ρ = density of air (kg/m3)
Note! The density of air varies with temperature. At 0 oC the density is 1.293 kg/m3. At 80 oC the density is 1.0 kg/m3.
It's common to express sensible heat flow rate as:
q = m cpa (tB - tA ) (3b)
or alternatively:
q = L ρ cpa (tB - tA ) (3c)
Heating Coil Effectiveness
For a limited heating coil surface the average surface temperature will always be higher than the outlet air temperature. The effectiveness of a heating coil can be expressed as:
μ = (tB - tA ) / (tHC - tA ) (4)
where
μ = heating coil effectiveness
tHC = mean surface temperature of the heating coil (oC)
Example - Heating Air
1 m3/s of air at 15 oC and relative humidity 60% (A) is heated to 30 oC (B). The surface temperature of the heating coil is 80 oC. The density of air at 20 oC is 1.205 kg/m3.
From the Mollier diagram the enthalpy in (A) is 31 kJ/kg and in (B) 46 kJ/kg.
The heating coil effectiveness can be calculated as:
μ = (30 oC - 15 oC) / (80 oC - 15 oC)
= 0.23
The heat flow can be calculated as:
q = (1 m3/s) (1.205 kg/m3) ((46 kJ/kg) - (31 kJ/kg))
= 18 (kJ/s, kW)
As an alternative, as one of the most common methods:
q = (1 m3/s) (1.205 kg/m3) (1.01 kJ/kg. oC) (30 oC - 15 oC)
= 18.3 (kJ/s, kW)
Note! Due to the inaccuracy when working with diagrams there is a small difference between the total heat flow and the sum of the latent and sensible heat. In general - this inaccuracy is within acceptable limits.



