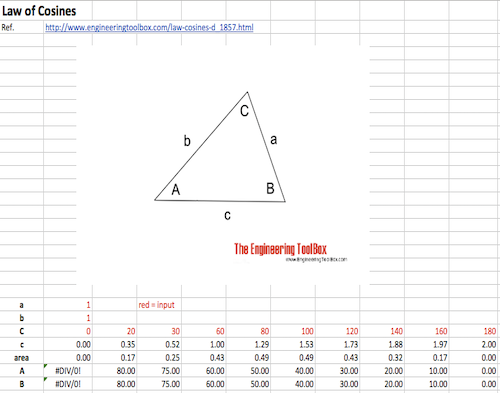
Law of Cosines
One side of a triangle when the opposite angle and two sides are known.
The "Law of Cosines" can be used to calculate one side of a triangle when the angle opposite and the other two sides are known.
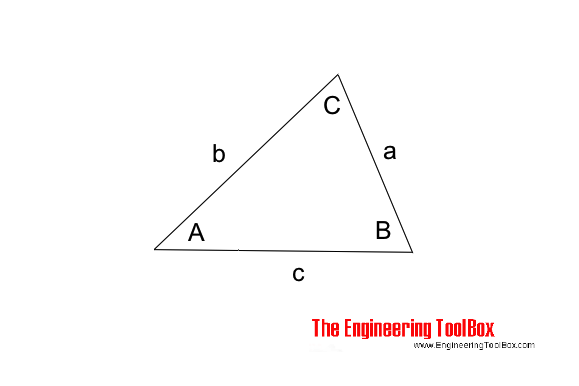
The "Law of Cosines" can be expressed as
$$ c^2 = a^2 + b^2 - 2 a b cos C \tag{1} $$
where
a, b and c = length of triangle sides (m, ft ..)
C = angle opposite side c (degrees)
Example - Calculate Side in Triangle
If side a = 1 m, side b = 1.3 m and angle C = 60 degrees - the side c can be calculated by modifying eq. 1 to
$$ c = \sqrt{ (1 m)^2 + (1.3 m)^2 - 2 (1 m) (1.3 m) cos (60 degrees) } = \underline{1.18} m $$
Law of Cosines Calculator
The generic calculator below can used to calculate the side c:
Law of Cosines - Excel Template
