Wire Rope Slings
Sling angles and influence on capacity.
Slings angles affects ropes capacities.
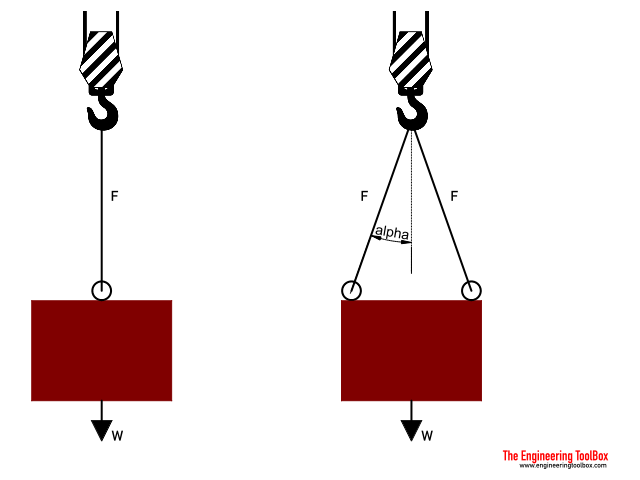
If angle - alpha - is measured between
- the vertical line (as with gravity force), and
- the rope or wire
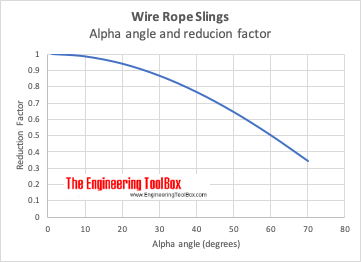
the relative capacity compared to a vertical straight lifting is reduced with reduction factor as indicated below.
f = cos(α) (1)
where
f = reduction factor
α = angle between vertical line and rope (degrees)
| Angle - α - (degrees) | Reduction Factor - f - |
|---|---|
| 0 | 1.000 |
| 10 | 0.985 |
| 20 | 0.940 |
| 30 | 0.866 |
| 40 | 0.766 |
| 50 | 0.643 |
| 60 | 0.500 |
| 70 | 0.342 |
Example - Capacity of a Single Rope or Wire
The capacity of a single rope that follows a vertical line is 100% since the reduction factor is 1.
If the weight of a body is W - the load in the wire is
F = W (2)
where
F = force in rope (N, lbf)
W = m g = weight of body (N, lbf)
m = mass of body (kg, slugs)
g = acceleration of gravity (9.81 m/s2, 32.17 ft/s2)
For a body with mass 100 kg the load in the rope can be calculated
F = (100 kg) (9.81 m/s2)
= 981 N
= 9.8 kN
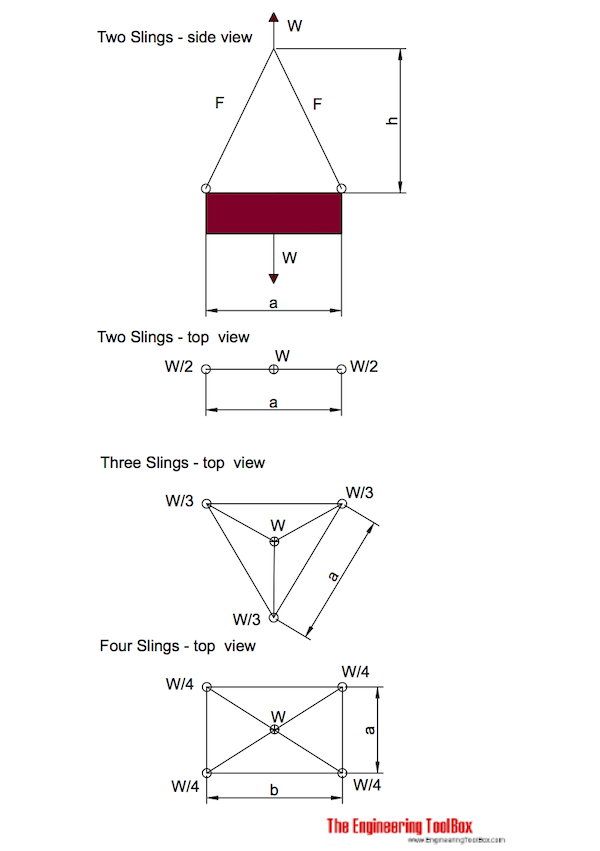
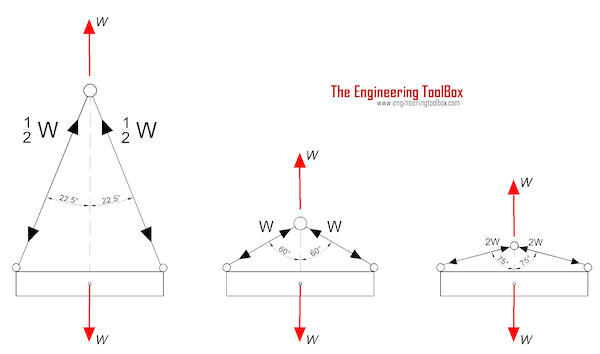
Example - Capacity of Two Ropes (or Wires)
Two wires or ropes follows the vertical line
The capacity of two wires that follows the vertical line is 100% since the reduction factor is 1.
If the weight of a body is W - the load in each wire is
F = W / 2 (3)
For a body with weight 1000 N the load in each rope can be calculated as
F = (1000 N) / 2
= 500 N
= 0.5 kN
Two wires - or ropes - with angle 30o to the vertical line
The capacity of two wires with angle 30o to the vertical line is 86.6% since the reduction factor is 0.866.
If the weight of a body is W - the load in each wire is
F = (W / 2) / cos(30o)
= (W / 2) / f
= (W / 2) / 0.866
= 0.577 W (4)
For a body with weight 1000 N the loads in the ropes can be calculated
F = 0.577 (1000 N)
= 577 N
= 0.58 kN
Wire Rope Slings Calculators
The calculators below can be used to calculate wire rope forces. Note that mass (kg) and not weight (N) is used as input.