Pythagorean Theorem
Verifying square corners.
Sponsored Links
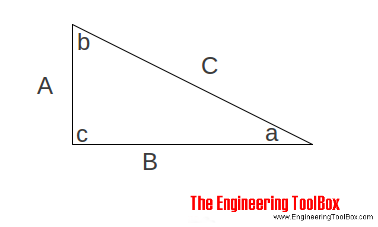
The Pythagorean theorem often used
- to verify if a corner is square (90 degrees)
and can be expressed as
C2 = A2 + B2 (1)
(1) can be transformed to express the length of hypotenuse C as
C = (A2 + B2)1/2 (1b)
Example - Determine the length of the Hypotenuse - C
With A = 5 m and B = 10 m - the length of the hypotenuse - C - can be calculated as
C = ((5 m)2 + (10 m)2)1/2
= 11.2 m
Squaring a Corner
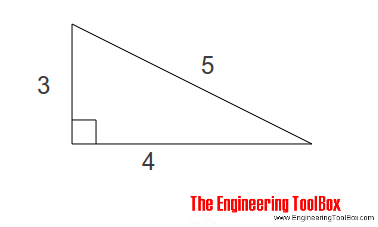
The angle is square (90 degrees) if
- A = 3 (m, ft)
- B = 4 (m, ft)
- C = 5 (m, ft)
Hypotenuse Calculator
Calculate square triangle hypotenuse - C - length:
A (m, mm, cm, in, ft)
B (m, mm, cm, in, ft)
The Sine Rule
A / sin a = B / sin b = C / sin c (2)
Sponsored Links
