Law of Tangents
Triangles and law of tangents.
The "Law of Tangents" can be used to calculate the angles or sides of a triangle.
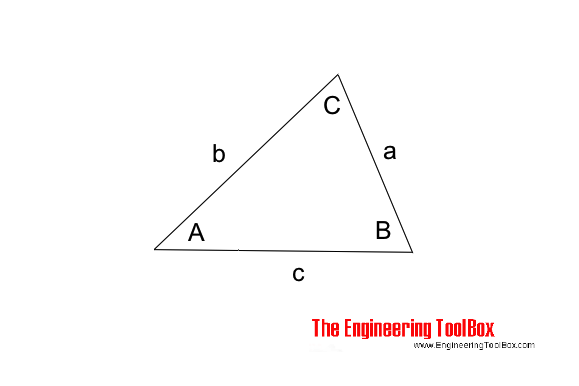
Law of Tangents
The "Law of Tangents" can be expressed as
(a + b) / (a - b) = tan(1/2 (A + B)) / tan(1/2 (A - B)) (1)
where
a, b and c = length of sides in triangle (m, ft ...)
A, B and C = angles in the triangle (degrees)
Pythagorean theorem
The Pythagorean theorem can be expressed as
a2 + b2 = c2 (2)
Law of sines
The Law of sines can be expressed as
a / sin(A) = b / sin(B) = c / sin(C) (3)
Angles
If the length of all three sides in the triangle are known - the angles can be calculated as
A = arccos((b2 + c2 - a2) / (2 b c)) (4a)
B = arccos((a2 + c2 - b2) / (2 a c)) (4b)
C = arccos((a2 + b2 - c2) / (2 a b)) (4c)



