Three-Phase Electrical Motors - Power Factor vs. Inductive Load
Inductive loads and power factors with electrical three-phase motors.
The power factor of an AC electric power system is defined as the ratio active (true or real) power to apparent power , where
- Active (Real or True) Power is measured in watts (W) and is the power drawn by the electrical resistance of a system doing useful work
- Apparent Power is measured in volt-amperes (VA) and is the voltage on an AC system multiplied by all the current that flows in it. It is the vector sum of the active and the reactive power
- Reactive Power is measured in volt-amperes reactive (VAR). Reactive Power is power stored in and discharged by inductive motors, transformers and solenoids
Reactive power is required for the magnetization of an electric motor but does not perform any work. Reactive power required by inductive loads increases the amounts of apparent power - and the required supply to the grid from the power supplier to the distribution system.
Increased reactive and apparent power will decrease the power factor - PF .
Power Factor
It is common to define the Power Factor - PF - as the cosine of the phase angle between voltage and current - or the " cosφ ":
PF = cos(φ) (1)
where
PF = power factor
φ = phase angle between voltage and current
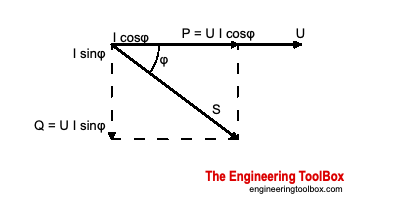
The power factor defined by IEEE and IEC is the ratio between the applied active (true) power - and the apparent power , and can in general be expressed as:
PF = P / S (2)
where
PF = power factor
P = active (true or real) power (Watts)
S = apparent power (VA, volts amps)
A low power factor is the result of inductive loads such as transformers and electric motors. Unlike resistance loads creating heat by consuming kilowatts, inductive loads require a current flow to create magnetic fields to produce the desired work.
Power factor is an important measurement in electrical AC systems because
- an overall power factor less than 1 indicates that the electricity supplier need to provide more generating capacity than actually required
- the current waveform distortion that contributes to reduced power factor is caused by voltage waveform distortion and overheating in the neutral cables of three-phase systems
International standards such as IEC 61000-3-2 have been established to control current waveform distortion by introducing limits for the amplitude of current harmonics.
Example - Power Factor
A industrial plant draws 200 A at 400 V and the supply transformer and backup UPS is rated 400 V x 200 A = 80 kVA .
If the power factor - PF - of the loads is 0.7 - only
80 kVA × 0.7
= 56 kW
of real power is consumed by the system. If the power factor is close to 1 (a purely resistive circuit) the supply system with transformers, cables, switch-gear and UPS could be made considerably smaller.
- Any power factor less than 1 means that the circuit's wiring has to carry more current than what would be necessary with zero reactance in the circuit to deliver the same amount of (true) power to the resistive load.
Conductor Cross-Section vs. Power Factor
Required cross-section area of conductor with lower power factor:
| Power Factor | 1 | 0.9 | 0.8 | 0.7 | 0.6 | 0.5 | 0.4 | 0.3 |
| Cross-Section | 1 | 1.2 | 1.6 | 2.04 | 2.8 | 4.0 | 6.3 | 11.1 |
A low power factor is expensive and inefficient and some utility companies may charge additional fees when the power factor is less than 0.95. A low power factor will reduce the electrical system's distribution capacity by increasing the current flow and causing voltage drops.
"Leading" or "Lagging" Power Factors
A Power Factor is usually stated as "leading" or "lagging" to show the sign of the phase angle.
- With a purely resistive load the current and voltage changes polarity in step and the power factor will be 1 . Electrical energy flows in a single direction across the network in each cycle.
- Inductive loads - transformers, motors and wound coils - consumes reactive power with current waveform lagging the voltage.
- Capacitive loads - capacitor banks or buried cables - generates reactive power with current phase leading the voltage.
Inductive and capacitive loads stores energy in magnetic or electric fields in the devices during parts of the AC cycles. The energy is returned back to the power source during the rest of the cycles.
In systems with mainly inductive loads - typically industrial plants with many electric motors - the lagging voltage are compensated with capacitor banks.
Power Factor for a Three-Phase Motor
The total power required by an inductive device like a motor or similar consists of
- Active (true or real) power (measured in kilowatts, kW)
- Reactive power - the nonworking power caused by the magnetizing current, required to operate the device (measured in kilovars, kVAR)
The power factor for a three-phase electric motor can be expressed as:
PF = P / ((3)1/2 U I) (3)
where
PF = power factor
P = power applied (W, watts)
U = voltage (V)
I = current (A, amps)
- or alternatively:
P = (3)1/2 U I PF
= (3)1/2 U I cos(φ) (3b)
U, l and cos φ are normally quoted on the motor nameplate.
Typical Motor Power Factors
| Power (hp) | Speed (rpm) | Power Factor (cos φ ) | ||||
|---|---|---|---|---|---|---|
| Unloaded | 1/4 load | 1/2 load | 3/4 load | full load | ||
| 0 - 5 | 1800 | 0.15 - 0.20 | 0.5 - 0.6 | 0.72 | 0.82 | 0.84 |
| 5 - 20 | 1800 | 0.15 - 0.20 | 0.5 - 0.6 | 0.74 | 0.84 | 0.86 |
| 20 - 100 | 1800 | 0.15 - 0.20 | 0.5 - 0.6 | 0.79 | 0.86 | 0.89 |
| 100 - 300 | 1800 | 0.15 - 0.20 | 0.5 - 0.6 | 0.81 | 0.88 | 0.91 |
- 1 hp = 745.7 W
Power Factor by Industry
Typical un-improved power factors:
| Industry | Power Factor |
|---|---|
| Brewery | 75 - 80 |
| Cement | 75 - 80 |
| Chemical | 65 - 75 |
| Electro-chemical | 65 - 75 |
| Foundry | 75 - 80 |
| Forging | 70 - 80 |
| Hospital | 75 - 80 |
| Manufacturing, machines | 60 - 65 |
| Manufacturing, paint | 65 - 70 |
| Metalworking | 65 - 70 |
| Mine, coal | 65 - 80 |
| Office | 80 - 90 |
| Oil pumping | 40 - 60 |
| Plastic production | 75 - 80 |
| Stamping | 60 - 70 |
| Steel works | 65 - 80 |
| Textiles | 35 - 60 |
Benefits of Power Factor Corrections
- reduced power bills - avoiding low power factor penalty from the utility power company
- increased system capacity - additional loads can be added without overloading the system
- improved system operating characteristics by reduced line loss - due to less current
- improved system operating characteristics by gaining voltage - excessive voltage drops are avoided
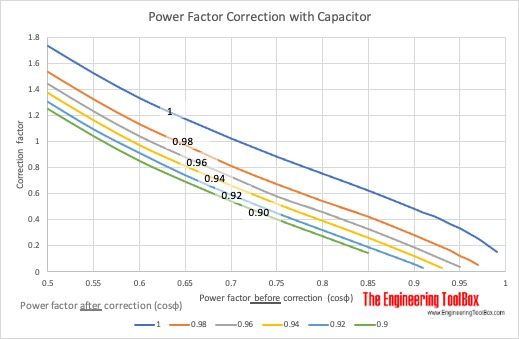
Power Factor Correction with Capacitor
Power factor before improvement (cosΦ) | Capacitor correction factor | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Power factor after improvement (cosΦ) | |||||||||||
| 1.0 | 0.99 | 0.98 | 0.97 | 0.96 | 0.95 | 0.94 | 0.93 | 0.92 | 0.91 | 0.90 | |
| 0.50 | 1.73 | 1.59 | 1.53 | 1.48 | 1.44 | 1.40 | 1.37 | 1.34 | 1.30 | 1.28 | 1.25 |
| 0.55 | 1.52 | 1.38 | 1.32 | 1.28 | 1.23 | 1.19 | 1.16 | 1.12 | 1.09 | 1.06 | 1.04 |
| 0.60 | 1.33 | 1.19 | 1.13 | 1.08 | 1.04 | 1.01 | 0.97 | 0.94 | 0.91 | 0.88 | 0.85 |
| 0.65 | 1.17 | 1.03 | 0.97 | 0.92 | 0.88 | 0.84 | 0.81 | 0.77 | 0.74 | 0.71 | 0.69 |
| 0.70 | 1.02 | 0.88 | 0.81 | 0.77 | 0.73 | 0.69 | 0.66 | 0.62 | 0.59 | 0.56 | 0.54 |
| 0.75 | 0.88 | 0.74 | 0.67 | 0.63 | 0.58 | 0.55 | 0.52 | 0.49 | 0.45 | 0.43 | 0.40 |
| 0.80 | 0.75 | 0.61 | 0.54 | 0.50 | 0.46 | 0.42 | 0.39 | 0.35 | 0.32 | 0.29 | 0.27 |
| 0.85 | 0.62 | 0.48 | 0.42 | 0.37 | 0.33 | 0.29 | 0.26 | 0.22 | 0.19 | 0.16 | 0.14 |
| 0.90 | 0.48 | 0.34 | 0.28 | 0.23 | 0.19 | 0.16 | 0.12 | 0.09 | 0.06 | 0.02 | |
| 0.91 | 0.45 | 0.31 | 0.25 | 0.21 | 0.16 | 0.13 | 0.09 | 0.06 | 0.02 | ||
| 0.92 | 0.43 | 0.28 | 0.22 | 0.18 | 0.13 | 0.10 | 0.06 | 0.03 | |||
| 0.93 | 0.40 | 0.25 | 0.19 | 0.15 | 0.10 | 0.07 | 0.03 | ||||
| 0.94 | 0.36 | 0.22 | 0.16 | 0.11 | 0.07 | 0.04 | |||||
| 0.95 | 0.33 | 0.18 | 0.12 | 0.08 | 0.04 | ||||||
| 0.96 | 0.29 | 0.15 | 0.09 | 0.04 | |||||||
| 0.97 | 0.25 | 0.11 | 0.05 | ||||||||
| 0.98 | 0.20 | 0.06 | |||||||||
| 0.99 | 0.14 | ||||||||||
Example - Improving power factor with capacitor
An electrical motor with power 150 kW has power factor before improvement cosΦ = 0.75 .
For a required power factor after improvement cosΦ = 0.96 - the capacitor correction factor is 0.58 .
The required KVAR capacity can be calculated as
C = (150 kW) 0.58
= 87 KVAR
Suggested Capacitor Ratings for T-Frame NEMA Class B Motors
Recommended sizes of KVAR units needed for correction of induction motors to approximately 95% power factor.
| Induction Motor Rating (HP) | Nominal Motor Speed (rpm) | |||||
|---|---|---|---|---|---|---|
| 3600 | 1800 | 1200 | ||||
| Capacitor Rating (KVAR) | Reduction of Line Current (%) | Capacitor Rating (KVAR) | Reduction of Line Current (%) | Capacitor Rating (KVAR) | Reduction of Line Current (%) | |
| 3 | 1.5 | 14 | 1.5 | 23 | 2.5 | 28 |
| 5 | 2 | 14 | 2.5 | 22 | 3 | 26 |
| 7.5 | 2.5 | 14 | 3 | 20 | 4 | 21 |
| 10 | 4 | 14 | 4 | 18 | 5 | 21 |
| 15 | 5 | 12 | 5 | 18 | 6 | 20 |
| 20 | 6 | 12 | 6 | 17 | 7.5 | 19 |
| 25 | 7.5 | 12 | 7.5 | 17 | 8 | 19 |
| 30 | 8 | 11 | 8 | 16 | 10 | 19 |
| 40 | 12 | 12 | 13 | 15 | 16 | 19 |
| 50 | 15 | 12 | 18 | 15 | 20 | 19 |
| 60 | 18 | 12 | 21 | 14 | 22.5 | 17 |
| 75 | 20 | 12 | 23 | 14 | 25 | 15 |
| 100 | 22.5 | 11 | 30 | 14 | 30 | 12 |
| 125 | 25 | 10 | 36 | 12 | 35 | 12 |
| 150 | 30 | 10 | 42 | 12 | 40 | 12 |
| 200 | 35 | 10 | 50 | 11 | 50 | 10 |
| 250 | 40 | 11 | 60 | 10 | 62.5 | 10 |
| 300 | 45 | 11 | 68 | 10 | 75 | 12 |
| 350 | 50 | 12 | 75 | 8 | 90 | 12 |
| 400 | 75 | 10 | 80 | 8 | 100 | 12 |
| 450 | 80 | 8 | 90 | 8 | 120 | 10 |
| 500 | 100 | 8 | 120 | 9 | 150 | 12 |