Heat Capacity
The amount of heat required to change the temperature of a substance by one degree.
Heat Capacity - C - is a characteristic of an object - the amount of heat required to change its temperature by one degree.
- Heat Capacity has the units of energy per degree.
The amount of heat supplied to heat an object can be expressed as:
Q = C dt (1)
where
Q = amount of heat supplied (J, Btu)
C = heat capacity of system or object (J/K, Btu/ oF)
dt = temperature change (K, C°, oF)
The SI unit for heat capacity is J/K (joule per kelvin). In the English system, the units are British thermal units per pound per degree Fahrenheit (Btu/oF). In some contexts kJ or cal and kcal are used instead of J.
Never use tabulated values of heat capacity without checking the unit of actual values!
Specific Heat Capacity (c) is the amount of heat required to change the temperature of a mass unit of a substance by one degree. Specific heat is a more common term for the same.
The heat supplied to a mass can be expressed as
dQ = m c dt (1)
where
dQ = heat supplied (J, kJ Btu)
m = unit mass (g, kg, lb)
c = specific heat (J/g K, kJ/kg oC, kJ/kg K, Btu/lb oF)
dt = temperature change (K, C°, oF)
(1) can be transferred to express Specific Heat as:
c = dQ / m dt (1b)
Example: The specific heat of iron is 0.45 J/(g K), which means that it takes 0.45 Joules of heat to raise one gram of iron by one degree Kelvin.
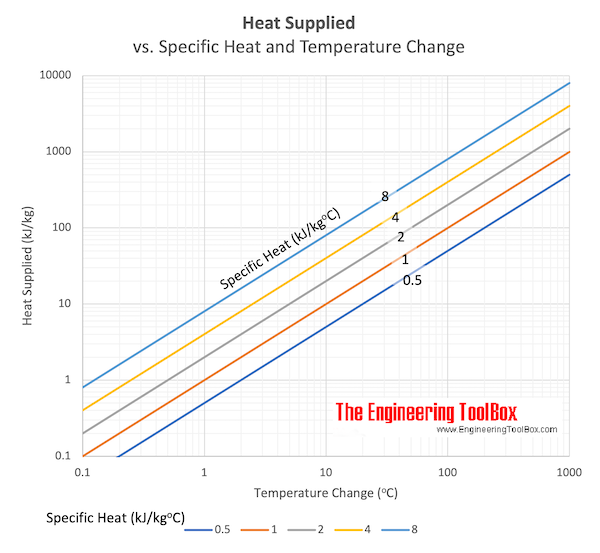
Download and print Heat supplied vs. Specfic heat and change in Temperature chart
Specific Heat Gases
There are two definitions of Specific Heat for vapors and gases:
cp = (δh / δT)p - Specific Heat at constant pressure (J/gK)
cv = ( δh / δT)v - Specific Heat at constant volume (J/gK)
For solids and liquids, cp = cv
Use the links to see tabulated values of specific heat of gases, common liquids and fluids, food and foodstuff, metals and semimetals, common solids and other common substances.
Gas Constant
The individual individual gas constant, R, can be expressed as
R = cp - cv (2)
Ratio of Specific Heat
The Ratio of Specific Heat is expressed as
k = cp / cv (3)
Molar Heat Capacity (Cp) is the amount of heat needed to increase the temperature of one mol of a substance by one degree at constant pressure.
It is expressed in joules per moles per degrees Kelvin (or Celsius), J/(mol K).
Example: The molar heat capacity of iron is 25.10 J/(mol K), which means that it takes 25.10 Joules of heat to raise 1 mol of iron by 1 degree Kelvin.
Tabulated values of molar heat capacity, Cp, of a lot of organic and inorganic substances can be found in Standard enthalpy of formation, Gibbs free energy of formation, entropy and molar heat capacity of organic substances and Standard state and enthalpy of formation, Gibbs free energy of formation, entropy and heat capacity, together with ΔH°f, ΔG°f and S° for the same substances at 25°C.
Converting between Specific heat and Molar heat capacity
The specific heat capacity can be calculated from the molar heat capacity, and vise versa:
cp = Cp / M and
Cp = cp . M
where
cp = specific heat capacity
Cp = molar heat capacity
M = molar weight of the actual substance (g/mol).
Example: Methanol (with molecular formula CH3OH) has a molar heat capacity, Cp, of 81.1 J/(mol K). What is the specific heat capacity, cp?
First, we calculate (or find) the molar weight of methanol: 1*12.01g/mol C + 4*1.008g/mol H + 1*16.00g/mol O = 32.04 g/mol CH3OH
Then, the specific heat capacity of methanol is: cp = 81.8 J/(molK) / 32.04 g/mol = 2.53 J/(g K)
Converting between commonly used Units
- 1 Btu/lbmoF = 4186.8 J/kg K = 1 kcal/kgoC
- Online Specific heat capacity unit converter
Example - Heating Aluminum
2 kg of aluminum is heated from 20 oC to 100 oC. Specific heat of aluminum is 0.91 kJ/kg0C and the heat required can be calculated as
dQ = (2 kg) (0.91 kJ/kg0C) ((100 oC) - (20 oC))
= 145.6 (kJ)
Example - Heating Water
One liter of water is heated from 0 oC to boiling 100 oC. Specific heat of water is 4.19 kJ/kg0C and the heat required can be calculated as
dQ = (1 litre) (1 kg/litre) (4.19 kJ/kg0C) ((100 oC) - (0 oC))
= 419 (kJ)
= 419 (kWs) (1/3600 h/s)
= 0.12 kWh
Related Topics
-
Basics
The SI-system, unit converters, physical constants, drawing scales and more. -
Material Properties
Material properties of gases, fluids and solids - densities, specific heats, viscosities and more. -
Thermodynamics
Work, heat and energy systems.
Related Documents
-
Acetone - Thermophysical Properties
Chemical, physical and thermal properties of acetone, also called 2-propanone, dimethyl ketone and pyroacetic acid. Phase diagram included. -
Ammonia - Specific Heat vs. Temperature and Pressure
Online calculator, figures and tables showing specific heat, CP and CV, of gasous and liquid ammonia at temperatures ranging from -73 to 425°C (-100 to 800°F) at pressure ranging from 1 to 100 bara (14.5 - 1450 psia) - SI and Imperial Units. -
Benzene - Thermophysical properties
Chemical, physical and thermal properties of benzene, also called benzol. Phase diagram included. -
Butane - Specific Heat vs. Temperature and Pressure
Online calculators, figures and tables showing specific heat, Cp and Cv, of gasous and liquid butane, C4H10, at varying temperarure and pressure, SI and Imperial units. -
Combustion Heat
Heat of combustion (energy content) for som common substances - with examples how to calculate heat of combustion. -
Energy Accumulated in Heated Water - kWh
The amount of thermal energy stored in heated water. -
Ethylene - Thermophysical Properties
Chemical, physical and thermal properties of ethylene, also called ethene, acetene and olefiant gas. Phase diagram included. -
Food and Foodstuff - Specific Heat
Specific heat of common food and foodstuff like apples, bass, beef, pork and many more. -
Gases - Ratios of Specific Heat
Ratios of specific heat for gases with constant pressure and volume processes. -
Gases - Specific Heats and Individual Gas Constants
Specific heat at constant volume, specific heat at constant pressure, specific heat ratio and individual gas constant - R - common gases as argon, air, ether, nitrogen and many more. -
Heat, Work and Energy
Heat vs. work vs. energy. -
Heavy Water - Thermophysical Properties
Thermodynamic properties of heavy water (D2O) like density, melting temperature, boiling temperature, latent heat of fusion, latent heat of evaporation, critical temperature and more. -
Liquids and Fluids - Specific Heats
Specific heats for some common liquids and fluids - acetone, oil, paraffin, water and many more. -
Metals - Specific Heats
Specific heat of commonly used metals like aluminum, iron, mercury and many more - imperial and SI units. -
Nitrogen - Thermal Diffusivity vs. Temperature and Pressure
Figures and tables showing thermal diffusivity of nitrogen at varying temperarure and pressure, SI and Imperial units. -
Phenols, alcohols and carboxylic acids - pKa values
For oxygen containing organic compounds this is given: pKa (the negative logarithm of the acid dissociation constant), molecular structures, molar weights, density and melting and boiling points. -
Solids - Specific Heats
Common solids - like brick, cement, glass and many more - and their specific heats - in Imperial and SI units. -
Specific Heat of common Substances
Specific heat of products like wet mud, granite, sandy clay, quartz sand and more. -
Standard enthalpy of formation, Gibbs energy of formation, entropy and molar heat capacity of organic substances
The standard enthalpy of formation, Gibbs energy of formation, entropy and molar heat capacity are tabulated for more than hundred organic substances. -
Standard State and Enthalpy of Formation, Gibbs Free Energy of Formation, Entropy and Heat Capacity
Definition and explanation of the terms standard state and standard enthalpy of formation, with listing of values for standard enthalpy and Gibbs free energy of formation, as well as standard entropy and molar heat capacity, of 370 inorganic compounds. -
Thermodynamic Key Values Internationally Agreed
Internationally agreed, internally consistent, values for the thermodynamic properties (standard enthalpy of formation, entropy and [H°(298)-H°(0)]) of key chemical substances. -
Thermodynamic Terms - Functions and Relations
Common thermodynamic terms and functions - potential energy, kinetic energy, thermal or internal energy, chemical energy, nuclear energy and more. -
Water - Specific Heat vs. Temperature
Online calculator, figures and tables showing specific heat of liquid water at constant volume or constant pressure at temperatures from 0 to 360 °C (32-700 °F) - SI and Imperial units. -
Water - Thermophysical Properties
Thermal properties of water at different temperatures like density, freezing temperature, boiling temperature, latent heat of melting, latent heat of evaporation, critical temperature and more.
