Stress in Thick-Walled Cylinders or Tubes

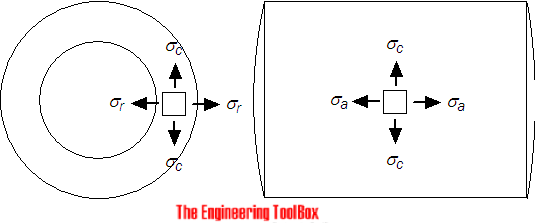
When a thick-walled tube or cylinder is subjected to internal and external pressure a hoop and longitudinal stress are produced in the wall.

Stress in Axial Direction

The stress in axial direction at a point in the tube or cylinder wall can be expressed as:

σ_a = (p_i r_i² - p_o r_o²) / (r_o² - r_i²)                                   (1)

where

σ_a = stress in axial direction (MPa, psi)

p_i = internal pressure in the tube or cylinder (MPa, psi)

p_o = external pressure in the tube or cylinder (MPa, psi)

r_i = internal radius of tube or cylinder (mm, in)

r_o = external radius of tube or cylinder (mm, in)

Stress in Circumferential Direction - Hoop Stress

The stress in circumferential direction - hoop stress - at a point in the tube or cylinder wall can be expressed as:

σ_c = ((p_i r_i² - p_o r_o²) / (r_o² - r_i²)) + (r_i² r_o² (p_i - p_o) / (r² (r_o² - r_i²)))                                    (2)

where

σ_c = stress in circumferential direction (MPa, psi)

r = radius to point in tube or cylinder wall (mm, in) (r_i < r < r_o)

maximum stress when  r = r_i (inside pipe or cylinder)

Resultant Stress

Combined stress in a single point in the cylinder wall cannot be described by a single vector using vector addition. Instead stress tensors (matrixes) describing the linear connection between two physical vectors quantities can be used.

Stress in Radial Direction

The stress in radial direction at a point in the tube or cylinder wall can be expressed as:

σ_r = ((p_i r_i² - p_o r_o²) / (r_o² - r_i²)) - (r_i² r_o² (p_i - p_o) / (r² (r_o² - r_i²)))                                  (3)

maximum stress when  r = r_i (outside pipe or cylinder)

Example  - Stress in Thick walled Cylinder

In a cylinder with inside diameter 200 mm (radius 100 mm) and outside diameter 400 mm (radius 200 mm) there is a pressure 100 MPa relative to the outside pressure. 

Stress in axial direction can be calculated as

σ_a = (((100 MPa) (100 mm)² - (0 MPa) (200 mm)²) / ((200 mm)² - (100 mm)²) 

   = 33.3 MPa      

Stress in circumferential direction - hoop stress - at the inside wall (100 mm) can be calculated as

σ_c = (((100 MPa) (100 mm)² - (0 MPa) (200 mm)²) / ((200 mm)² - (100 mm)²)) + ((100 mm)² (200 mm)² ((0 MPa) - (100 MPa)) / ((100 mm)² ((200 mm)² - (100 mm)²))) 

    = 167 MPa      

Stress in radial direction at the inside wall (100 mm) can be calculated as

σ_r = (((100 MPa) (100 mm)² - (0 MPa) (200 mm)²) / ((200 mm)² - (100 mm)²)) - ((100 mm)² (200 mm)² ((0 MPa)- (100 MPa)) / ((100 mm)² ((200 mm)² - (100 mm)²))) 

    = -100 MPa  

Note! - that in addition stress caused by pressure - stress can be induced in the pipe or cylinder wall by restricted temperature expansion.

Online Thick Walled Pipe & Cylinder Calculator

The calculator below can be used to calculate the stress in thick walled pipes or cylinders with closed ends.

inside pressure (MPa, psi)

outside pressure (MPa, psi)

inside radius (mm, in)

outside radius (mm, in)

radius to point in the wall (mm, in)