Rotating Bodies - Stress
Stress in rotating disc and ring bodies.
Stress in a Rotating Disc
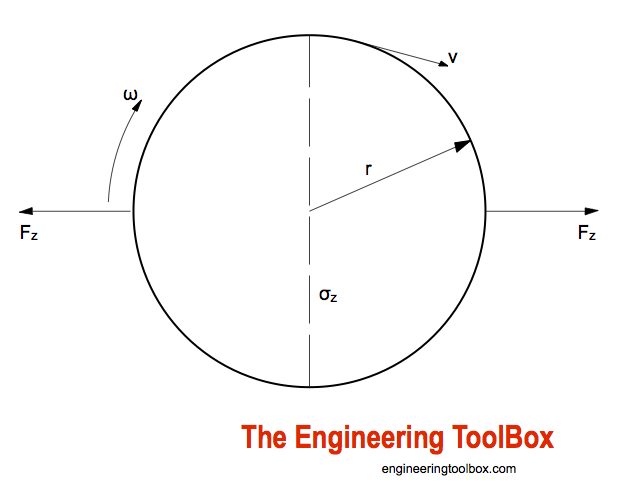
Stress in a rotating disc can be calculated as
σz = ω2r2ρ / 3
= v2ρ / 3
= ( 2 π n / 60)2r2ρ / 3 (1)
where
σz = stress (Pa, N/m2)
ω = angular velocity (rad/s)
r = radius of disc (m)
ρ = density (kg/m3 )
π = 3.14...
n= revolutions per minute (rpm)
Stress in a Rotating Ring
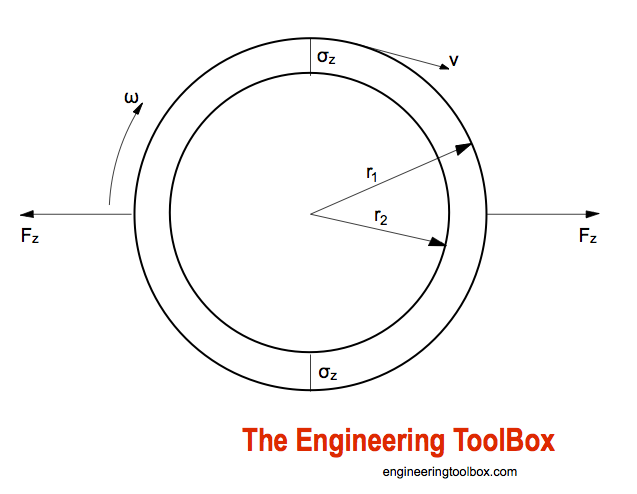
Stress in a rotating ring can be calculated as
σz = ω2ρ ( r12+ r1 r2+ r2 2 ) / 3 (2)
where
r1 = outer radius of ring (m)
r2= inner radius of ring (m)
For a thin ring the equation can be simplified to
σz = ω2ρ r 2 (3)
where
r = mean radius of ring (m)
Design Stress for materials used in Flywheels
| Material | Density (kg/m3 ) | Typical Design Stress ( MPa) |
|---|---|---|
| Aluminum alloy | 2700 | |
| Birch plywood | 700 | 30 |
| Composite carbon fiber - 40% epoxy | 1550 | 750 |
| E-glass fiber - 40% epoxy | 1900 | 250 |
| Kevlar fiber - 40% epoxy | 1400 | 1000 |
| Maraging steel | 8000 | 900 |
| Titanium Alloy | 4500 | 650 |
| "Super paper" | 1100 | |
| S-glass fiber/epoxy | 1900 | 350 |
Related Topics
-
Dynamics
Motion of bodies and the action of forces in producing or changing their motion - velocity and acceleration, forces and torque.
Related Documents
-
Centripetal and Centrifugal Acceleration Force
Forces due to circular motion and centripetal / centrifugal acceleration. -
Flywheels - Kinetic Energy
The kinetic energy stored in flywheels - the moment of inertia. -
Stress
Stress is force applied on cross-sectional area. -
Stress in Thick-Walled Cylinders or Tubes
Radial and tangential stress in thick-walled cylinders or tubes with closed ends - with internal and external pressure. -
Stress in Thin-Walled Cylinders or Tubes
Hoop and longitudinal stress thin-walled tubes or cylinders. -
Stress, Strain and Young's Modulus
Stress is force per unit area - strain is the deformation of a solid due to stress. -
Young's Modulus, Tensile Strength and Yield Strength Values for some Materials
Young's Modulus (or Tensile Modulus alt. Modulus of Elasticity) and Ultimate Tensile Strength and Yield Strength for materials like steel, glass, wood and many more.
