AC Circuits - Power vs. Voltage and Current
The alternating current In an AC circuit is generated by a sinusoidal voltage source.
In an AC circuit - alternating current is generated from a sinusoidal voltage source
Voltage
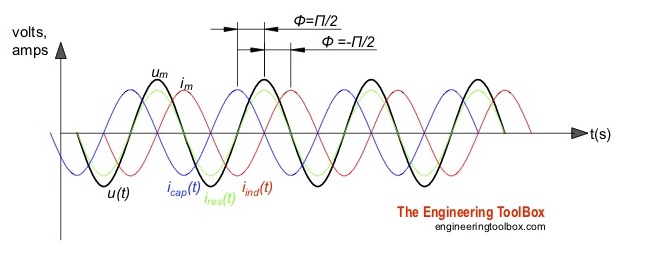
Currents in circuits with pure resistive , capacitive or inductive loads.
The momentary voltage in an sinusoidal AC circuit can be expressed on the time-domain form as
u(t) = Umax cos(ω t + θ) (1)
where
u(t) = voltage in the circuit at time t (V)
Umax = maximal voltage at the amplitude of the sinusoidal wave (V)
t = time (s)
ω = 2 π f
= angular frequency of sinusoidal wave (rad /s)
f = frequency (Hz, 1/s)
θ = phase shift of the sinusoidal wave (rad)
The momentary voltage can alternatively be expressed in the frequency-domain (or phasor) form as
U = U(jω)
= Umax ejθ (1a)
where
U(jω) = U = complex voltage (V)
A phasor is a complex number expressed in polar form consisting of a magnitude equal to the peak amplitude of the sinusoidal signal and a phase angle equal to the phase shift of the sinusoidal signal with reference to a cosine signal.
Note that the specific angular frequency - ω - is not explicitly used in the phasor expression.
Current
The momentary current can be expressed can be expressed in the time-domain form as
i(t) = Im cos(ω t + θ) (2)
where
i(t) = current at time t (A)
Imax = maximal current at the amplitude of the sinusoidal wave (A)
Currents in circuits with pure resistive, capacitive or inductive loads are indicated in the figure above. The current in a "real" circuit with resistive, inductive and capacitive loads are indicated in the figure below.
The momentary current in an AC circuit can alternatively be expressed in the frequency-domain (or phasor) form as
I = I(jω) = Imax ejθ (2a)
where
I = I(jω) = complex current (A)
Frequency
Note that the frequency of most AC systems are fixed - like 60 Hz in North America and 50 Hz in most of the rest of the world.
The angular frequency for North America is
ω = 2 π 60
= 377 rad/s
The angular frequency for most of the rest of the world is
ω = 2 π 50
= 314 rad/s
Resistive Load
The voltage over a resistive load in an AC system can be expressed as
U = R I (4)
where
R = resistance (ohm)
For a resistance load in an AC circuit the voltage is in phase with the current.
Inductive Load
The voltage over an inductive load in an AC system can be expressed as
U = j ω L I (5)
where
L = inductance (henry)
For an inductive load the current in an AC circuit is π/2 (90o) phase after the voltage (or voltage before the current).
Capacitive Load
The voltage over an inductive load in an AC system can be expressed as
U = 1 / (j ω C) I (6)
where
C = capacitance (farad)
For a capacitive load the current in an AC circuit leads the voltage by π/2 (90o) phase .
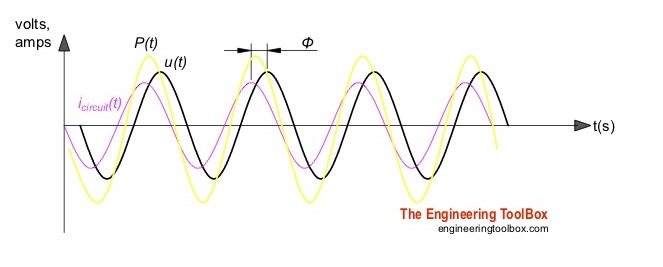
In a real electrical circuit there is a mix of resistive, capacitive and inductive loads with a voltage/current phase shift in the range - π/2 <= φ <= π/2 as illustrated in the figure below.
The current in a "real" circuit with a mix of resistive, inductive and capacitive loads. φ is the phase angle between the current and the voltage.
Impedance
Ohm's law for complex alternating current can be expressed as
Uz = Iz Z (7)
where
Uz = voltage drop over the load (volts, V)
Iz = current through the load (ampere, A)
Z = impedance of the load (ohms, Ω)
The impedance in an AC circuit can be regarded as complex resistance. The impedance acts as a frequency dependent resistor where the resistance is a function of the frequency of the sinusoidal excitation.
Impedances in Serie
The resulting impedance for impedances in series can be expressed as
Z = Z1 + Z2 (7b)
Impedances in Parallel
The resulting impedance for impedances in parallel can be expressed as
1 / Z = 1 / Z1 + 1 / Z2 (7c)
Admittance
Admittance is the inverted impedance
Y = 1 / Z (8)
where
Y = admittance (1/ohm)
RMS or Effective Voltage
The RMS value is the effective value of a sinusoidal voltage or current.
RMS - Root Mean Square - or effective voltage can be expressed as
Urms = Ueff
= Umax / (2)1/2
= 0.707 Umax (9)
where
Urms = Ueff
= RMS voltage (V)
Umax = maximum voltage (amplitude) of sinusoidal voltage source (V)
RMS - Root Mean Square - or effective current can be expressed as
Irms = Ieff
= Imax / (2)1/2
= 0.707 Imax (10)
where
Irms = Ieff
= RMS current (A)
Imax = maximum current (amplitude) of sinusoidal voltage source (A)
AC voltmeters and ammeters shows the RMS value of the voltage or current - or 0.707 times the max peak values. The max peak values are 1.41 times the voltmeter values.
Example
- for a 230V system the Urms = 230V and Umax = 324 V
- for a 120V system the Urms = 120V and Umax = 169 V
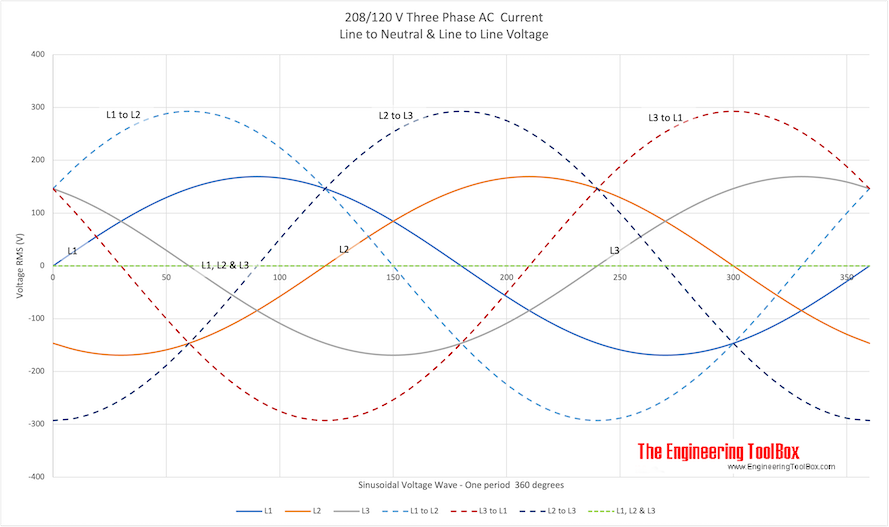
AC Three Phase Voltage - Line to Line and Line to Neutral
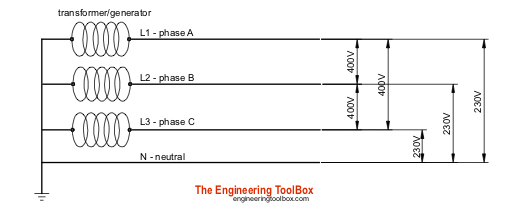
In an AC three phase system the voltage can be delivered between the lines and the neutral (phase potential), or between the lines (line potential). The resulting voltages for two common systems - the European 400/230V and the North American 208/120V system are indicated for one period in the figures below.
400V/230V AC
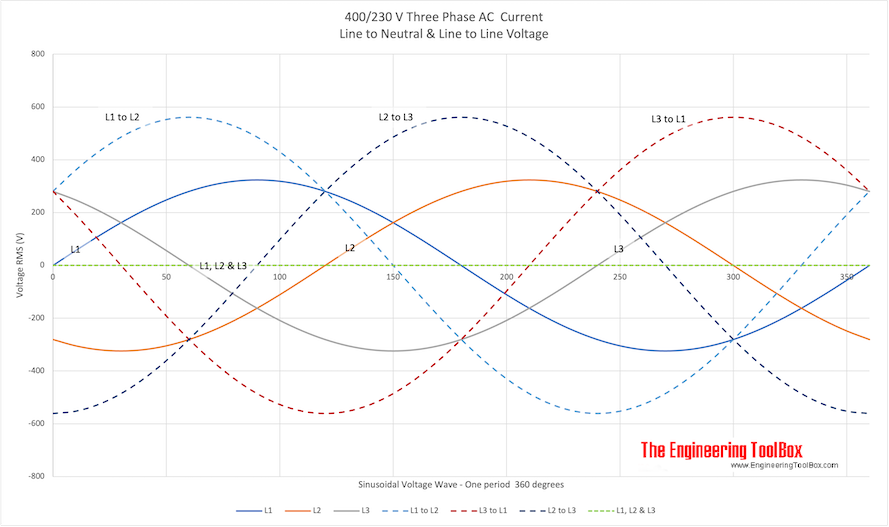
print 400/230V Three Phase Diagram
- L1, L2 and L3 are the three phases line to to neutral potentials - phase potentials
- L1 to L2, L1 to L3 and L2 to L3 are the three phases line to line potentials - line potentials
- L2, L2 and L3 is the resulting potential of the tree phases in a balanced circuit - resulting potential = 0
The magnitude of the line potentials is equal to 31/2 (1.73) the magnitude of the phase potential.
Urms, line = 1.73 Urms, phase (11)
208V/120V AC
print 208/120V Three Phase Diagram
Power
Active - or real or true - power that do the actual work in the circuit - can be calculated as
P = Urms Irms cos(φ) (12)
where
P = active real power (W)
φ = the phase angle between the current and the voltage (rad, degrees)
Cos φ is also called the Power Factor.
Reactive power in the circuit can be calculated as
Q = Urms Irms sin(φ) (13)
Q = reactive power (VAR)