Pumps - NPSH (Net Positive Suction Head)
An introduction to pumps and the Net Positive Suction Head (NPSH).
Low pressure at the suction side of a pump may cause the fluid to start boiling with
- reduced efficiency
- cavitation
- damage
of the pump as a result. Boiling starts when the pressure in the liquid is reduced to the vapor pressure of the fluid at the actual temperature.
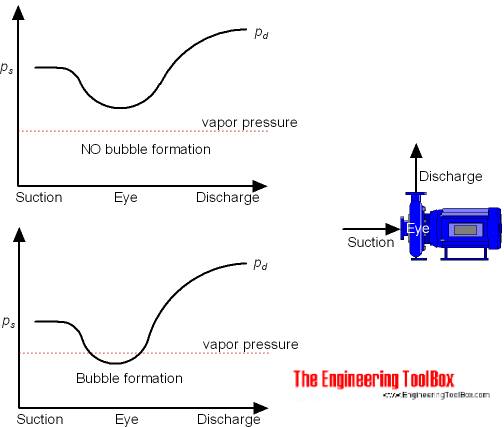
To characterize the potential for boiling and cavitation the difference between
- the total head on the suction side of the pump - close to the impeller, and
- the liquid vapor pressure at the actual temperature
can be used.
Suction Head
Based on the Energy Equation - the suction head in the fluid close to the impeller*) can be expressed as the sum of the static and velocity head:
hs = ps / γliquid + vs2 / 2 g (1)
where
hs = suction head close to the impeller (m, in)
ps = static pressure in the fluid close to the impeller (Pa (N/m2), psi (lb/in2))
γliquid = specific weight of the liquid (N/m3, lb/ft3)
vs = velocity of fluid (m/s, in/s)
g = acceleration of gravity (9.81 m/s2, 386.1 in/s2)
*) We can not measure the suction head "close to the impeller". In practice we can measure the head at the pump suction flange. Be aware that - depending of the design of the pump - the contribution to the NPSH value from the suction flange to the impeller can be substantial.
Liquids Vapor Head
The liquids vapor head at the actual temperature can be expressed as:
hv = pv / γvapor (2)
where
hv = vapor head (m, in)
pv = vapor pressure (m, in)
γvapor = specific weight of the vapor (N/m3, lb/ft3)
Note! The vapor pressure in a fluid depends on the temperature. Water, our most common fluid, starts boiling at 20 oC if the absolute pressure is 2.3 kN/m2. For an absolute pressure of 47.5 kN/m2 the water starts boiling at 80 oC. At an absolute pressure of 101.3 kN/m2 (normal atmosphere) the boiling starts at 100 oC.
Net Positive Suction Head - NPSH
The Net Positive Suction Head - NPSH - can be defined as
- the difference between the Suction Head, and
- the Liquids Vapor Head
and can be expressed as
NPSH = hs - hv (3)
or, by combining (1) and (2)
NPSH = ps / γ + vs2 / 2 g - pv / γ (3b)
where
NPSH = Net Positive Suction Head (m, in)
Available NPSH - NPSHa or NPSHA
The Net Positive Suction Head available from the application to the suction side of a pump is often named NPSHa. The NPSHa can be estimated during the design and the construction of the system, or determined experimentally by testing the actual physical system.
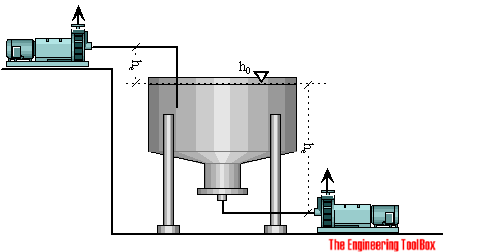
The available NPSHa can be estimated with the Energy Equation.
For a common application - where the pump lifts a fluid from an open tank at one level to an other, the energy or head at the surface of the tank is the same as the energy or head before the pump impeller and can be expressed as:
h0 = hs + hl (4)
where
h0 = head at surface (m, in)
hs = head before the impeller (m, in)
hl = head loss from the surface to impeller - major and minor loss in the suction pipe (m, in)
In an open tank the head at the surface can be expressed as:
h0 = p0 / γ
= patm / γ (4b)
For a closed pressurized tank the absolute static pressure inside the tank must be used.
The head before the impeller can be expressed as:
hs = ps / γ + vs2 / 2 g + he (4c)
where
he = elevation from surface to pump - positive if pump is above the tank, negative if the pump is below the tank (m, in)
Transforming (4) with (4b) and (4c):
patm / γ = ps / γ + vs2 / 2 g + he+ hl (4d)
The head available before the impeller can be expressed as:
ps / γ + vs2 / 2 g = patm / γ - he- hl (4e)
or as the available NPSHa:
NPSHa = patm / γ - he - hl - pv / γ (4f)
where
NPSHa = Available Net Positive Suction Head (m, in)
Available NPSHa - the Pump is above the Tank
If the pump is positioned above the tank, the elevation - he - is positive and the NPSHa decreases when the elevation of the pump increases (lifting the pump).
At some level the NPSHa will be reduced to zero and the fluid will start to evaporate.
Available NPSHa - the Pump is below the Tank
If the pump is positioned below the tank, the elevation - he - is negative and the NPSHa increases when the elevation of the pump decreases (lowering the pump).
It's always possible to increase the NPSHa by lowering the pump (as long as the major and minor head loss due to a longer pipe don't increase it more). Note! It is important - and common - to lower a pump when pumping a fluid close to evaporation temperature.
Required NPSH - NPSHr or NPSHR
The NPSHr, called as the Net Suction Head as required by the pump in order to prevent cavitation for safe and reliable operation of the pump.
The required NPSHr for a particular pump is in general determined experimentally by the pump manufacturer and a part of the documentation of the pump.
The available NPSHa of the system should always exceeded the required NPSHr of the pump to avoid vaporization and cavitation of the impellers eye. The available NPSHa should in general be significant higher than the required NPSHr to avoid that head loss in the suction pipe and in the pump casing, local velocity accelerations and pressure decreases, start boiling the fluid on the impellers surface.
Note that required NPSHr increases with the square of capacity.
Pumps with double-suction impellers has lower NPSHr than pumps with single-suction impellers. A pump with a double-suction impeller is considered hydraulically balanced but is susceptible to an uneven flow on both sides with improper pipe-work.
Example - Pumping Water from an Open Tank
When elevating a pump located above a tank (lifting the pump) - the fluid starts to evaporate at the suction side of the pump at what is the maximum elevation for the actual temperature of the pumping fluid.
At the maximum elevation NPSHa is zero. The maximum elevation can therefore be expressed by modifying (4f) to:
NPSHa = patm / γ - he - hl - pv / γ
= 0
For an optimal theoretical condition we neglect major and minor head loss. The elevation head can then be expressed as:
he = patm / γ - pv / γ (5)
The maximum elevation - or suction head - for an open tank depends on the atmospheric pressure - which in general can be regarded as constant, and the vapor pressure of the fluid - which in general vary with temperature, especially for water.
The absolute vapor pressure of water at temperature 20 oC is 2.3 kN/m2. The maximum theoretical elevation of a pump when pumping water at 20 oC is therefore:
he = (101.33 kN/m2) / (9.80 kN/m3) - (2.3 kN/m2) / (9.80 kN/m3)
= 10.1 m
Due to head loss in the suction pipe and the local conditions inside the pump - the theoretical maximum elevation normally is significantly decreased.
Maximum theoretical elevation of a pump above an open tank at different water temperatures are indicated below.
Suction Head and Reduction in Suction Lift for Water and Temperature
Suction head for water - or max. elevation of a pump above a water surface - is affected by the temperature of the water - as indicated below:
| Temperature | abs Vapor Pressure | Reduction in Suction Lift | Suction Head |
|---|---|---|---|
| (oC) | (kN/m2, kPa) | (m) | (m) |
| 0 | 0.6 | 0 | 10.3 |
| 5 | 0.9 | 0 | 10.2 |
| 10 | 1.2 | 0 | 10.2 |
| 15 | 1.7 | 0 | 10.2 |
| 20 | 2.3 | 0.1 | 10.1 |
| 25 | 3.2 | 0.2 | 10.0 |
| 30 | 4.3 | 0.3 | 9.9 |
| 35 | 5.6 | 0.4 | 9.8 |
| 40 | 7.7 | 0.7 | 9.5 |
| 45 | 9.6 | 0.8 | 9.4 |
| 50 | 12.5 | 1.1 | 9.1 |
| 55 | 15.7 | 1.5 | 8.7 |
| 60 | 20 | 1.9 | 8.3 |
| 65 | 25 | 2.3 | 7.8 |
| 70 | 32.1 | 3.1 | 7.1 |
| 75 | 38.6 | 3.8 | 6.4 |
| 80 | 47.5 | 4.7 | 5.5 |
| 85 | 57.8 | 5.8 | 4.4 |
| 90 | 70 | 7.0 | 3.2 |
| 95 | 84.5 | 8.5 | 1.7 |
| 100 | 101.33 | 10.2 | 0 |
Note! - as indicated in the table above hot water can be difficult to pump. To limit cavitation in a hot water system
- locate the pump in lowest possible position
- if possible - increase the static pressure in system
- oversize and simplify the piping on the suction side of the pump to limit friction and dynamic losses
Reduction in Suction Lift for Water vs. Altitude
| Altitude (m) | Reduction in Suction Lift (m) |
|---|---|
| 0 | 0 |
| 250 | 0.30 |
| 500 | 0.60 |
| 750 | 0.89 |
| 1000 | 1.16 |
| 1250 | 1.44 |
| 1500 | 1.71 |
| 1750 | 1.97 |
| 2000 | 2.22 |
| 2250 | 2.47 |
| 2500 | 2.71 |
Pumping Hydrocarbons
Note that the NPSH specifications provided by manufacturers in general are for use with cold water. For hydrocarbons these values must be lowered to account for vapor release properties of complex organic liquids.
| Fluid | Temperature (oC) | abs Vapor Pressure (kPa) |
|---|---|---|
| Ethanol | 20 | 5.9 |
| 65 | 58.2 | |
| Methyl Acetate | 20 | 22.8 |
| 55 | 93.9 |
The head developed by a pump is independent of liquid and a performance curve for water can be used for Newtonian liquids like gasoline, diesel or similar. Note that the required power to the pump depends on the liquid density and must be recalculated.
NPSH and Liquids with Dissolved Gas
NPSH calculations might be modified if there is significant amount of dissolved gas in a liquid. The gas saturation pressure is often much higher than a liquid's vapor pressure.



