Static Pressure vs. Head
Static pressure vs. pressure head in fluids.
Pressure indicates the normal force per unit area at a given point acting on a given plane. Since there is no shearing stresses present in a fluid at rest - the pressure in a fluid is independent of direction.
For fluids - liquids or gases - at rest the pressure gradient in the vertical direction depends only on the specific weight of the fluid.
How pressure changes with elevation in a fluid can be expressed as
Δp = - γ Δh (1)
where
Δ p = change in pressure (Pa, psi)
Δ h = change in height (m, in)
γ = specific weight of fluid (N/m3, lb/ft3 )
The pressure gradient in vertical direction is negative - the pressure decrease upwards.
Specific Weight
Specific Weight of a fluid can be expressed as:
γ = ρ g (2)
where
ρ = density of fluid (kg/m3, slugs /ft3 )
g = acceleration of gravity (9.81 m/s2, 32.174 ft/s2)
In general the specific weight - γ - is constant for fluids. For gases the specific weight - γ - varies with elevation (and compression).
The pressure exerted by a static fluid depends only upon
- the depth of the fluid
- the density of the fluid
- the acceleration of gravity
Static Pressure in a Fluid
For a incompressible fluid - as a liquid - the pressure difference between two elevations can be expressed as:
Δ p = p2- p1
= - γ (h2- h1 ) (3)
where
p2= pressure at level 2 (Pa, psi)
p1 = pressure at level 1 (Pa, psi)
h2= level 2 (m, ft)
h1 = level 1 (m, ft)
(3) can be transformed to:
Δ p = p1 - p 2
= γ (h2- h1 ) (4)
or
p1 - p2= γ Δ h (5)
where
Δ h = h2- h1 = difference in elevation - the dept down from location h2to h1 (m, ft)
or
p1 = γ Δ h + p2(6)
Example - Pressure in a Fluid
The absolute pressure at water depth of 10 m can be calculated as:
p1 = γ Δ h + p2
= (1000 kg/m3 ) (9.81 m/s2) (10 m) + (101.3 kPa)
= (98100 kg/ms2or Pa) + (101300 Pa)
= 199400 Pa
= 199.4 kPa
where
ρ = 1000 kg/m3
g = 9.81 m/s2
p2= pressure at surface level = atmospheric pressure = 101.3 kPa
The gauge pressure can be calculated by setting p2= 0
p1 = γ Δ h + p2
= (1000 kg/m3 ) (9.81 m/s2) (10 m)
= 98100 Pa
= 98.1 kPa
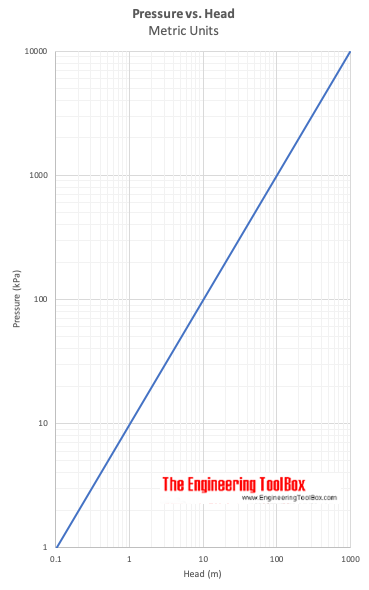
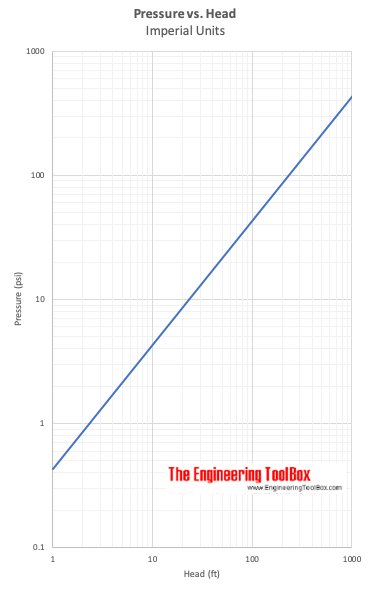
Pressure vs. Head
(6) can be transformed to:
Δ h = (p2- p1 ) / γ (7)
Δ h express head - the height difference of a column of fluid of specific weight - γ - required to give a pressure difference Δp = p2- p1 .
Example - Pressure vs. Head
A pressure difference of 5 psi (lbf /in2) is equivalent to head in water
(5 lbf /in2) (12 in/ft) (12 in/ft) / (62.4 lb/ft3 )
= 11.6 ft of water
or head in Mercury
(5 lbf /in2) (12 in/ft) (12 in/ft) / (847 lb/ft3 )
= 0.85 ft of mercury
Specific weight of water is 62.4 (lb/ft3 ) and specific weight of mercury is 847 (lb/ft3 ) .
Related Topics
-
Fluid Mechanics
The study of fluids - liquids and gases. Involving velocity, pressure, density and temperature as functions of space and time. -
Pumps
Design of pumping systems and pipelines. With centrifugal pumps, displacement pumps, cavitation, fluid viscosity, head and pressure, power consumption and more.
Related Documents
-
Darcy-Weisbach Equation - Major Pressure and Head Loss due to Friction
The Darcy-Weisbach equation can be used to calculate the major pressure and head loss due to friction in ducts, pipes or tubes. -
Efficiency in Pumps or Fans
The overall pump and fan efficiency is the ratio power gained by the fluid to the shaft power supplied. -
Hydropower
Power potential vs. head and flow rate. -
Hydrostatic Pressure vs. Depth
Depth and hydrostatic pressure. -
PE, PEH and PVC Pipes - Pressure Loss vs. Water Flow Diagram
Pressure loss (bar/100 m) and velocy in PE, PEH or PVC pipes with water flow. -
Potential Energy - Hydropower
Elevation and potential energy in hydropower. -
Pressure Gradient Diagrams
Static pressure graphical presentation throughout a fluid flow system. -
Pressure to Head Unit Converter
Pressure vs. head units - like lb/in2, atm, inches mercury, bars, Pa and more. -
Pumps - Head vs. Pressure
Converting head (ft or m) to pressure (psi or bar, kg/cm2) and vice versa. -
Pumps - NPSH (Net Positive Suction Head)
An introduction to pumps and the Net Positive Suction Head (NPSH). -
Pumps - Parallel vs. Serial Arrangement
Adding head and flowrate for pumps arranged in parallel vs. serial. -
Pumps - Suction Head vs. Altitude
The suction head of a water pump is affected by its operating altitude. -
Pumps and Fans - Energy Equation and Head Rise
The energy equation can be used to calculate the head rise in pumps and fans. -
System Curve and Pump Performance Curve
Utilize the system curve and the pump performance curve to select the proper pump for a particular application. -
Types of Fans - Capacity Ranges
Centrifugal, axial and propeller fans and their capacity ranges. -
Velocity Pressure Head
Dynamic pressure or velocity head. -
Water Pressure vs. Head
Pressure in pounds per square inch (psi) vs. head in feet of water (ft h2o).




