Pumps - Affinity Laws
Turbo machines affinity laws can be used to calculate volume capacity, head or power consumption in centrifugal pumps when changing speed or wheel diameters.
The Affinity Laws of centrifugal pumps or fans indicates the influence on volume capacity, head (pressure) and/or power consumption of a pump or fan due to
- change in speed of wheel - revolutions per minute (rpm)
- geometrically similarity - change in impeller diameter
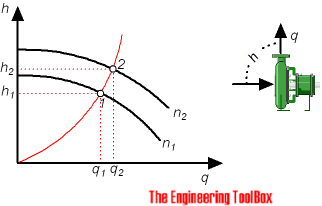
Note that there are two sets of affinity laws:
- affinity laws for a specific centrifugal pump - to approximate head, capacity and power curves for different motor speeds and /or different diameter of impellers
- affinity laws for a family of geometrically similar centrifugal pumps - to approximate head, capacity and power curves for different motor speeds and /or different diameter of impellers
Pump Affinity Laws for a Specific Centrifugal Pump
Volume Capacity
The volume capacity of a centrifugal pump can be expressed like
q1 / q2= (n1 / n2) (d1 / d2) (1)
where
q = volume flow capacity (m3 /s, gpm, cfm, ..)
n = wheel velocity - revolution per minute - (rpm)
d = wheel diameter (m, ft)
Head or Pressure
The head or pressure of a centrifugal pump can be expressed like
dp1 / dp2= (n1 / n2)2(d1 / d2)2(2)
where
dp = head or pressure (m, ft, Pa, psi, ..)
Power
The power consumption of a centrifugal pump can be expressed as
P1 / P2= (n1 / n2)3 (d1 / d2)3 (3)
where
P = power (W, bhp, ..)
Changing Wheel Velocity
If the wheel diameter is constant - change in pump wheel velocity can simplify the affinity laws to
Volume Capacity
q1 / q2= (n1 / n2) (1a)
Head or Pressure
dp1 / dp2= (n1 / n2)2(2a)
Power
P1 / P2= (n1 / n2)3 (3a)
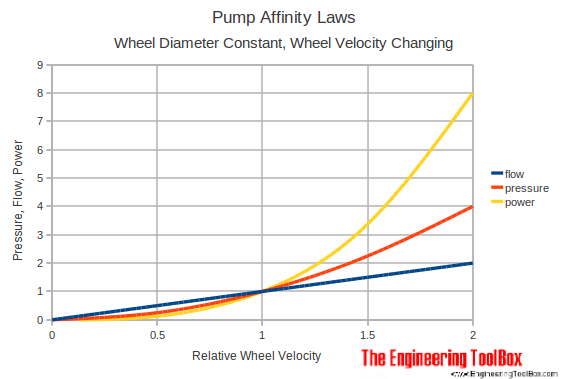
Note! If the speed of a pump is increased with 10%
- the volume flow increases with 10%
- the head increases with 21%
- the power increases with 33 %
If we want to increase the volume flow capacity of an existing system with 10% we have to increase the power supply with 33% .
Pump Affinity Laws Calculator - Changing Wheel Velocity
Replace the default values with the actual values. The calculator is generic and can be used with all common units as long as the use is consistent.
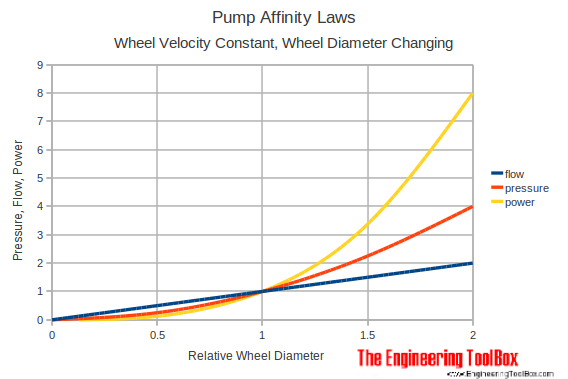
Changing the Impeller Diameter
If wheel velocity is constant a change in impeller diameter simplifies the affinity laws to
Volume Capacity
q1 / q2= d1 / d2(1b)
Head or Pressure
dp1 / dp2= (d1 / d2)2(2b)
Power
P1 / P2= (d1 / d2)3 (3b)
Pump Affinity Laws Calculator - Changing Wheel Diameter
Replace the default values with the actual values. The calculator is generic and can be used with all common units as long as the use of units is consistent.
Example - Pump Affinity Laws - Changing Pump Speed
The pump speed is changed when the impeller size is constant. The initial flow is 100 gpm , the initial head is 100 ft , the initial power is 5 bhp , the initial speed is 1750 rpm and the final speed 3500 rpm .
The final flow capacity can be calculated with (1a):
q2= q1 n2/ n1
= (100 gpm) (3500 rpm) / (1750 rpm)
= 200 gpm
The final head can be calculated with (2a):
dp2= dp1 (n2/ n1 )2
= (100 ft) ((3500 rpm) / (1750 rpm))2
= 400 ft
The final power consumption can be calculated with (3a):
P2= P1 (n2/ n1 )3
= (5 bhp) ((3500 rpm) / (1750 rpm))3
= 40 bhp
Example - Pump Affinity Laws - Changing Impeller Diameter
The diameter of the pump impeller is reduced when the pump speed is constant. The diameter is changed from 8 to 6 inches .
The final flow capacity can be calculated with (1b) :
q2= q1 (d2/ d1 )
= (100 gpm) ((¨6 in) / (8 in))
= 75 gpm
The final head can be calculated with (2b) :
dp2= dp1 (d2/ d1 )2
= (100 ft) ((6 in) / (8 in))2
= 56.3 ft
The final power consumption can be calculated with (3b) :
P2= P1 (d2/ d1 )3
= (5 bhp) ((6 in) / (8 in))3
= 2.1 bhp
Pump Affinity Laws for a Family of Geometrically Similar Pumps
The volume capacity can be expressed like
q1 / q2= (n1 / n2)(d1 / d2)3 (4)
where
q = volume flow capacity (m3 /s, gpm, cfm, ..)
n = wheel velocity - revolution per minute - (rpm)
d = wheel diameter
Head or Pressure
The head or pressure of a centrifugal pump can be expressed like
dp1 / dp2= (n1 / n2)2(d1 / d2)2(5)
where
dp = head or pressure (m, ft, Pa, psi, ..)
Power
The power consumption of a centrifugal pump can be expressed as
P1 / P2= (n1 / n2)3 (d1 / d2)5 (6)
where
P = power (W, bhp, ..)
Note that the affinity laws for fans are not identical with pumps.
Related Topics
-
Fluid Mechanics
The study of fluids - liquids and gases. Involving velocity, pressure, density and temperature as functions of space and time. -
Pumps
Design of pumping systems and pipelines. With centrifugal pumps, displacement pumps, cavitation, fluid viscosity, head and pressure, power consumption and more.
Related Documents
-
Centrifugal Pumps
An introduction to Centrifugal Pumps. -
Centrifugal Pumps - Capacity Modulation
Modulating pumps to adapt capacities to variable process demands. -
Centrifugal Pumps - Minimum Flow
Minimum continuous flow to prevent flashing in centrifugal pumps. -
Centrifugal Pumps - Shut-Off Head
Centrifugal pumps and maximum shut-off head. -
Fan Affinity Laws
The affinity laws can be used to calculate resulting volume capacity, head or power consumption when speed or wheel diameters are changed. -
Pumping Water - Required Horsepower
Horsepower required to pump water. -
Pumps - NPSH (Net Positive Suction Head)
An introduction to pumps and the Net Positive Suction Head (NPSH). -
Pumps - Specific Speed
Characterizing of impeller types in pumps in a unique and coherent manner. -
Pumps - Suction Specific Speed
Suction Specific Speed can be used to determine stable and reliable operations for pumps with max efficiency without cavitation.
