Drag Coefficient
The drag coefficient quantifies the drag or resistance of an object in a fluid environment.
Any object moving through a fluid experiences drag - the net force in the direction of flow due to pressure and shear stress forces on the surface of the object.
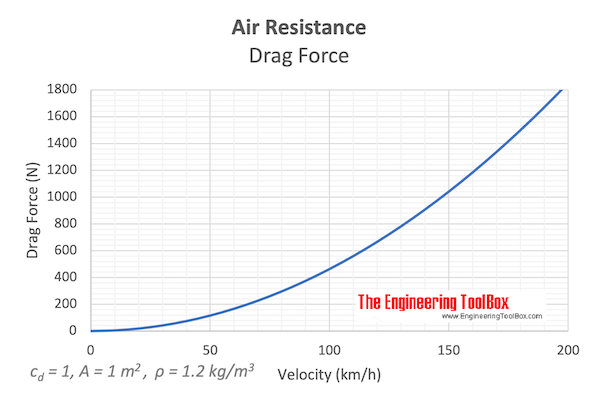
The drag force can be expressed as:
Fd = cd 1/2 ρ v2 A (1)
where
Fd = drag force (N)
cd = drag coefficient
ρ = density of fluid (1.2 kg/m3 for air at NTP)
v = flow velocity (m/s)
A = characteristic frontal area of the body (m2)
The drag coefficient is a function of several parameters like shape of the body, Reynolds Number for the flow, Froude number, Mach Number and Roughness of the Surface.
The characteristic frontal area - A - depends on the body.
Objects drag coefficients are mostly results of experiments. The drag coefficients for some common bodies are indicated below:
| Type of Object | Drag Coefficient - cd - | Frontal Area |
|---|---|---|
| Laminar flat plate (Re=106) | 0.001 | |
| Dolphin | 0.0036 | wetted area |
| Turbulent flat plate (Re=106) | 0.005 | |
| Subsonic Transport Aircraft | 0.012 | |
| Supersonic Fighter,M=2.5 | 0.016 | |
| Streamlined body | 0.04 | π / 4 d2 |
| Airplane wing, normal position | 0.05 | |
| Sreamlined half-body | 0.09 | |
| Long stream-lined body | 0.1 | |
| Bicycle - Streamlined Velomobile | 0.12 | 5 ft2 (0.47 m2) |
| Airplane wing, stalled | 0.15 | |
| Modern car like a Tesla model 3 or model Y | 0.23 | |
| Toyota Prius, Tesla model S | 0.24 | frontal area |
| Tesla model X | ||
| Sports car, sloping rear | 0.2 - 0.3 | frontal area |
| Common car like Opel Vectra (class C) | 0.29 | frontal area |
| Hollow semi-sphere facing stream | 0.38 | |
| Bird | 0.4 | frontal area |
| Solid Hemisphere | 0.42 | π / 4 d2 |
| Sphere | 0.5 | |
| Saloon Car, stepped rear | 0.4 - 0.5 | frontal area |
| Bike - Drafting behind an other cyclist | 0.5 | 3.9 ft2 (0.36 m2) |
| Convertible, open top | 0.6 - 0.7 | frontal area |
| Bus | 0.6 - 0.8 | frontal area |
| Old Car like a T-ford | 0.7 - 0.9 | frontal area |
| Cube | 0.8 | s2 |
| Bike - Racing | 0.88 | 3.9 ft2 (0.36 m2) |
| Bicycle | 0.9 | |
| Tractor Trailed Truck | 0.96 | frontal area |
| Truck | 0.8 - 1.0 | frontal area |
| Person standing | 1.0 – 1.3 | |
| Bike - Upright Commuter | 1.1 | 5.5 ft2 (0.51 m2) |
| Thin Disk | 1.1 | π / 4 d2 |
| Solid Hemisphere flow normal to flat side | 1.17 | π / 4 d2 |
| Squared flat plate at 90 deg | 1.17 | |
| Wires and cables | 1.0 - 1.3 | |
| Person (upright position) | 1.0 - 1.3 | |
| Hollow semi-cylinder opposite stream | 1.2 | |
| Ski jumper | 1.2 - 1.3 | |
| Hollow semi-sphere opposite stream | 1.42 | |
| Passenger Train | 1.8 | frontal area |
| Motorcycle and rider | 1.8 | frontal area |
| Long flat plate at 90 deg | 1.98 | |
| Rectangular box | 2.1 |
Example - Air Resistance Force acting on a Normal Car
The force required to overcome air resistance for a normal family car with drag coefficient 0.29 and frontal area 2 m2 in 90 km/h can be calculated as:
Fd = 0.29 1/2 (1.2 kg/m3) ((90 km/h) (1000 m/km) / (3600 s/h))2 (2 m2)
= 217.5 N
- compare car air resistance with car rolling resistance
The work done to overcome the air resistance in one hour driving (90 km) can be calculated as
Wd = (217.5 N) (90 km) (1000 m/km)
= 19575000 (Nm, J)
The power required to overcome the air resistance when driving 90 km/h can be calculated as
Pd = (217.5 N) (90 km/h) (1000 m/km) (1/3600 h/s)
= 5436 (Nm/s, J/s, W)
= 5.4 (kW)
Related Topics
-
Fluid Mechanics
The study of fluids - liquids and gases. Involving velocity, pressure, density and temperature as functions of space and time.
Related Documents
-
Car - Required Power and Torque
Power, torque, efficiency and wheel force acting on a car. -
Car Fuel Consumption - liter/100 km
Calculate fuel consumption in liter per km - consumption chart and calculator. -
Cars - New vs. Old Car Cost Calculator
Calculate and compare the costs between owning a new vs. an old car. -
Driving Distances between European Cities
Driving distance between some major European cities. -
Friction - Friction Coefficients and Calculator
Friction theory with calculator and friction coefficients for combinations of materials like ice, aluminum, steel, graphite and many more. -
Froude Number
Introduction to the Froude Number. -
Fuel Consumption - mpg
Calculate fuel consumption in miles per gallon - mpg - calculator and consumption charts. -
Liquids - Kinematic Viscosities
Kinematic viscosities of some common liquids like motor oil, diesel fuel, peanut oil and many more. -
Piston Engines - Compression Ratios
Cylinder volume and compression ratios in piston engines. -
Piston Engines - Displacement
Calculate piston engine displacement. -
Rolling Resistance
Rolling friction and rolling resistance. -
Target - Volume Flow Meters
Introduction to the target flow meters principles. -
Vehicle - Distance Traveled vs. Velcocity and Time Used (mph)
Speed (mph) and time (hours) and distance traveled (miles) chart. -
Vehicle - Distance Traveled vs. Velocity and Time (km/h)
Speed (km/h) vs. time (hours) and distance traveled (km). -
Viscosity Converting Chart
Convert between viscosity units like Centiposes, milliPascal, CentiStokes and SSU. -
Wind Load vs. Wind Speed
Wind load on surface - Wind load calculator.