Cartesian Coordinate System - Distance and Intermediate Position Between Two Points
Distance and intermediate position between two point in a cartesian x and y coordinate system.
In the rectangular Cartesian coordinate system the coordinate axes are perpendicular to one another and the same unit length is chosen on the two axes.
The distance between two points in Cartesian x and y coordinate system can be calculated as
$$ d(P_1, P_2) = \sqrt{(x_2 - x_1)^2 + (y_2 - y_1)^2} \tag{1}$$
Example - Distance between two points
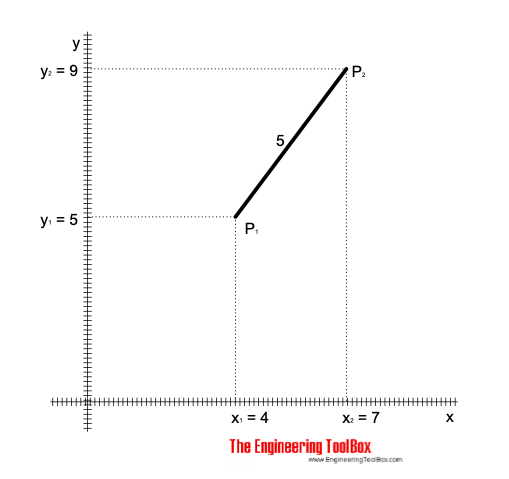
For point P1 the coordinates are x1 = 4, y1 = 5, and for point P2 the coordinates are x2 = 7, y2 = 9.
The distance between the points can be calculated as
$$ d(P_1, P_2) = \sqrt{(7 - 4)^2 + (9 - 5)^2} = \underline {5} $$
Intermediate position between two points
The intermediate position between two point in the cartesian coordinate system can be calculated as
$$ x ={ (r_1 x_1 + r_2 x_2) \over (r_1 + r_2)} \tag{2}$$
$$ y = {(r_1 y_1 + r_2 y_2) \over (r_1 + r_2) }\tag{3}$$
where
r1 = ratio of the distance between P1 to P - to the distance of P1 to P2
r2 = ratio of the distance between P2 to P - to the distance of P1 to P2
For the midpoint between P1 and P2:
$$ r_1 = r_2 = 1 \tag{4}$$
- and eq. 2 and 3 can be expressed as
$$ x ={ (x_1 + x_2) \over 2} \tag{2a}$$
$$ y = {(y_1 + y_2) \over 2}\tag{3a}$$
Example - Midpoint on Line
The midpoint on the line in the example above can be calculated as
$$ x ={ (4 + 7) \over 2 } = \underline {5.5} $$
$$ y = {(5 + 9) \over 2 } = \underline {7} $$



