Oblique Triangle
Calculate oblique triangles.
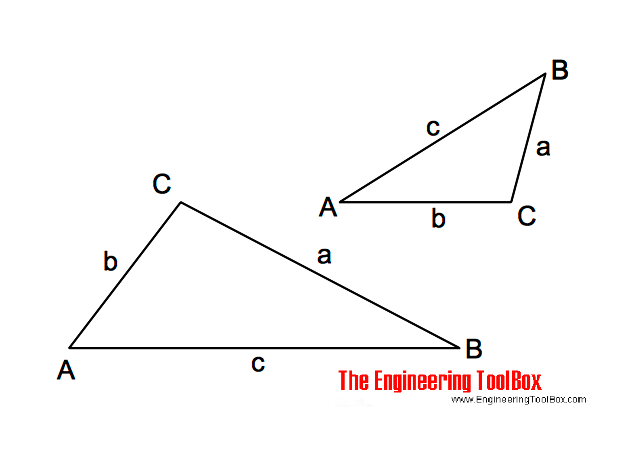
An oblique triangle is any triangle that is not a right angled triangle.
Triangle Three Known Values - Length and Angle Calculator
Calculate the unknown lengths and angles in a triangle. Add three known values - leave the rest of the inputs blank.
Note! - the calculator is based on the same value combinations used in the equations below. Other value combinations will not work - most triangles with three known values can be adapted to these equations. The calculator is quite simple. With strange results - check your input values.
Angle A (degrees)
Angle B (degrees)
Angle C (degrees)
Length a (m, mm, ft, in ..)
Length b (m, mm, ft, in ..)
Length c (m, mm, ft, in ..)
Area (m2, mm2, ft2, in2 .....):
(enable pop-up)
A, B and a is known, calculate
b = a sin(B) / sin(A) (1a)
C = 180o - (A + B) (1b)
c = a sin(C) / sin(A) (1c)
A, a and b is known, calculate
sin(B) = b sin(A) / a (2a)
C = 180o - (A + B) (2b)
c = a sin(C) / sin(A) (2c)
a, b and C is known, calculate
tan(A) = a sin(C) / (b - a cos(C)) (3a)
B= 180o - (A + C) (3b)
c = a sin(C) / sin(A) (3c)
a, b and c is known, calculate
cos(A) = (b2 + c2 - a2) / (2 b c) (4a)
cos(B)= (a2 + c2 - b2) / (2 a c) (4b)
C = 180o - (A + B) (4c)
a, b, c, A, B and C is known, calculate area
s = (a + b + c) / 2 (5a)
area = (s (s - a) (s- b) (s - c))1/2 (5b)
area = b c sin(A) / 2 (5c)
area = a2 sin(B) sin(C) / (2 sin(A)) (5d)
