Inorganic Acids and Bases - pKa Values
Values for the negative logarithm of the acid dissociation constant, pKa, of inorganic acids and bases, as well as hydrated metal ions.
Definitions of the acid dissociation constant and pKa are given below the table.
pKa values given in the table are measuered at 25°C, unless other temperature(°C) is indicated with superscript at the pKa value.
See also Acid-base properties of aqueous solutions of salts with ions from both acids and bases, Buffer solutions, pKa of amines, diamines and cyclic organic nitrogen compounds, pKa of phenols, alcohols and carboxylic acids and acid and base pH indicators
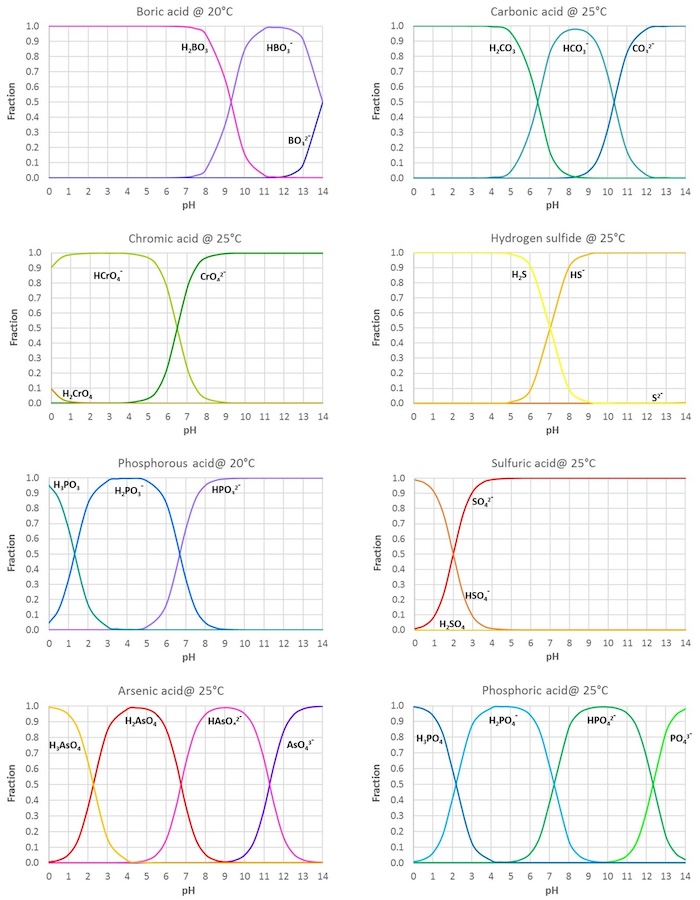
Below the table, figures showing the fractions of the different acid forms in aqueous solutions at varying pH are given for some common acids (values calculated from the tabulated pKas).
NB! For bases, the dissosiation constant is given in terms of the pKa value of their conjugated acid, BH+. These values are marked with an *.
| Acid name | Formula | pKa1 | pKa2 | pKa3 | pKa4 |
|---|---|---|---|---|---|
| Monoprotic acids | |||||
| Ammonia | NH3 | 9.24* | |||
| Arsenious acid | H3AsO3 | 9.29 | |||
| Boric acid | H3BO3 | 9.24 | |||
| Chlorous acid | HClO2 | 1.94 | |||
| Cyanic acid | HOCN | 3.46 | |||
| Hydrazoic acid | HN3 | 4.72 | |||
| Hydrazine | N2H4 | 8.1* | |||
| Hydrobromic acid | HBr | -9 | |||
| Hydrochloric acid | HCl | -7 | |||
| Hydrocyanic acid | HCN | 9.21 | |||
| Hydrofluoric acid | HF | 3.17 | |||
| Hydroiodic acid | HI | -10 | |||
| Hydrogen peroxide | H2O2 | 11.65 | |||
| Hydroxylamine | H2NOH | 5.94 | |||
| Hypobromous acid | HOBr | 8.62 | |||
| Hypochlorous acid | HOCl | 7.54 | |||
| Hypoiodous acid | HOI | 10.64 | |||
| Hypophosphorous acid | H3PO2 | 1.23 | |||
| Iodic acid | HIO3 | 0.78 | |||
| Nitrous acid | HNO2 | 3.25 | |||
| Nitric acid | HNO3 | -1.37 | |||
| Perchloric acid | HClO4 | -1.620 | |||
| Periodic acid | HIO4 | 1.64 | |||
| Sulfamic acid | H2NSO3H | 1.05 | |||
| Tetrafluoroboric acid | HBF4 | 0.5 | |||
| Thiocyanic acid | HSCN | -1.8 | |||
| Water | H2O | 13.995 | |||
| Diprotic acids | |||||
| Boric acid | H3BO3 | 9.2720 | 1420 | ||
| Carbonic acid | H2CO3 | 6.35 | 10.33 | ||
| Chromic acid | H2CrO4 | -0.98 | 6.49 | ||
| Germanic acid | H2GeO3 | 9.01 | 12.3 | ||
| Hydrogen selenide | H2Se | 3.89 | 11.0 | ||
| Hydrogen sulfide | H2S | 7.02 | 19 | ||
| Hydrogen telluride | H2Te | 2.618 | 11 | ||
| Phosphorous acid | H3PO3 | 1.320 | 6.720 | ||
| Selenous acid | H2SeO3 | 2.62 | 8.32 | ||
| Selenic acid | H2SeO4 | <0 | 1.7 | ||
| Silicic acid | H2SiO3 | 9.91 | 11.81 | ||
| Sulfurous acid | H2SO3 | 1.85 | 7.20 | ||
| Sulfuric acid | H2SO4 | -3 | 1.99 | ||
| Tellur(VI)ic acid | H6TeO6 | 7.6818 | 1118 | ||
| Tellurous acid | H2TeO3 | 6.27 | 8.43 | ||
| Triprotic acids | |||||
| Arsenic acid | H3AsO4 | 2.26 | 6.76 | 11.29 | |
| Phosphoric acid | H3PO4 | 2.16 | 7.21 | 12.32 | |
| Tetraprotic acids | |||||
| Pyrophosphoric acid | H4P2O7 | 0.91 | 2.10 | 6.70 | 9.32 |
| Orthosilicic acid | H4SiO4 | 9.930 | 11.830 | 1230 | 1230 |
| Hydrated metal ions | |||||
| Aluminium (III) ion | Al3+ | 4.85 | |||
| Barium (II) ion | Ba2+ | 13.4 | |||
| Beryllium(II) ion | Be2+ | 5.7 | |||
| Calcium(II) ion | Ca2+ | 12.6 | |||
| Chromium (III) ion | Cr3+ | 3.95 | |||
| Copper (II) ion | Ba2+ | 7.34 | |||
| Iron (III) ion | Fe3+ | 2.17 | |||
| Lead (II) ion | Ba2+ | 7.8 | |||
| Lithium (I) ion | Li+ | 13.8 | |||
| Magnesium (II) ion | Mg2+ | 11.4 | |||
| Manganese (II) ion | Mn2+ | 10.59 | |||
| Nickel (II) ion | Ni2+ | 9.86 | |||
| Sodium (I) ion | Na2+ | 14.8 | |||
| Scandium (III) ion | Sc3+ | 4.61 | |||
| Strontium (II) ion | Sr2+ | 13.2 | |||
| Uranium (IV) ion | U4+ | 0.68 | |||
| Vanadium (III) ion | V3+ | 2.9 | |||
| Zinc (II) ion | Zn2+ | 8.96 | |||
An acid dissociation constant, Ka, is a quantitative measure of the strength of an acid in solution. It is the equilibrium constant for a chemical reaction known as dissociation of acid–base reactions. In aqueous solution, the equilibrium of acid dissociation can be written symbolically as:
HA + H2O = A- +H3O+
where HA is an acid that dissociates into A-, (known as the conjugate base of the acid) and a hydrogen ion which combines with a water molecule to make a hydronium ion.
The chemical species HA, A- and H3O+ are said to be in equilibrium when their concentrations do not change with the passing of time. The dissociation constant is usually written as a quotient of the equilibrium concentrations (in mol/L), denoted by (HA), (A-) and (H3O+)
Ka = (A-)*(H3O+) / (HA)*(H2O)
In all, but the most concentrated, aqueous solutions of an acid the concentration of water can be taken as constant and can be ignored. The definition can then be written more simply
HA = A- + H+ and Ka = (A-)*(H+) / (HA)
This is the definition in common usage. For many practical purposes it is more convenient to discuss the logarithmic constant, pKa
pKa = -log10 Ka
The larger the value of pKa, the smaller the extent of dissociation at any given pH - that is, the weaker the acid.
A weak acid has a pKa value in the approximate range -2 to 12 in water.
Strong acids has pKa values of less than about -2; the dissociation of a strong acid is effectively complete such that concentration of the undissociated acid is too small to be measured. pKa values for strong acids can, however, be estimated by theoretical means.
After rearranging the expression defining Ka, and putting pH = -log10(H+), one obtains
pH = pKa + (A-) / (HA) and further
pH - pKa = log(A-) / (HA)
Then, a solution with 50% dissociation has pH equal to the pKa of the acid.
Polyprotic acids are acids that can lose more than one proton. Then we have more than one dissiciation constant; Ka1, Ka2, etc.. and similar pKa1, pKa2, etc.
All data given in the figures apply to dilute aqueous solutions at ambient temperature.
For bases, the pka value is given for the conjugate bases BH+ and BH22+.
BH+ = B + H+
The pKb for a base may be calculated from the pKa value of its conjugate acid:
pKw = pKa + pKb
At 25°C the pKw is 14 and
pKb = 14 - pKa
The figure below shows the fractions of the different acid forms (H2A, HA- and A2-for twoprotic acids) of di- and triprotic acids in aqueous solutions at varying pH: