Orifice, Nozzle, and Venturi Flow Meters: Principles, Calculations & Data
The orifice, nozzle and venturi flow rate meters makes the use of the Bernoulli Equation to calculate fluid flow rate using pressure difference through obstructions in the flow.
In a flow metering device based on the Bernoulli Equation the downstream pressure after an obstruction will be lower than the upstream pressure before. To understand orifice, nozzle and venturi meters it is necessary to explore the Bernoulli Equation.
The Bernoulli Equation
Assuming a horizontal flow (neglecting the minor elevation difference between the measuring points) the Bernoulli Equation can be modified to:
p1 + 1/2 ρ v12 = p2 + 1/2 ρ v22 (1)
where
p = pressure (Pa, psf (lb/ft2))
ρ = density (kg/m3, slugs/ft3)
v = flow velocity (m/s, ft/s)
The equation can be adapted to vertical flow by adding elevation heights:
p1 + 1/2 ρ v12 + γ h1 = p2 + 1/2 ρ v22 + γ h2 (1b)
where
γ = specific weight of fluid (kg/m3, slugs/ft3)
h = elevation (m, ft)
Assuming uniform velocity profiles in the upstream and downstream flow - the Continuity Equation can be expressed as
q = v1 A1
= v2 A2 (2)
where
q = flow rate (m3/s, ft3/s)
A = flow area (m2, ft2)
Combining (1) and (2), assuming A2 < A1, gives the "ideal" equation:
q = A2 (2(p1 - p2) / ρ (1 - (A2 / A1)2))1/2 (3)
For a given geometry (A), the flow rate can be determined by measuring the pressure difference p1 - p2.
The theoretical flow rate q will in practice be smaller (2 - 40%) due to geometrical conditions.
The ideal equation (3) can be modified with a discharge coefficient:
q = cd A2 (2 (p1 - p2) / ρ (1 - (A2 / A1)2))1/2 (3b)
where
cd = discharge coefficient
The discharge coefficient cd is a function of the jet size - or orifice opening - the
area ratio = Avc / A2
where
Avc = area in "vena contracta" (m2, ft2)
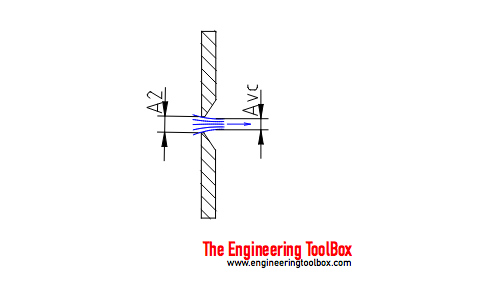
"Vena Contracta" is the minimum jet area that appears just downstream of the restriction. The viscous effect is usually expressed in terms of the non-dimensional parameter Reynolds Number - Re.
Due to the Benoulli and the Continuity Equation the velocity of the fluid will be at it's highest and the pressure at the lowest in "Vena Contracta". After the metering device the velocity will decrease to the same level as before the obstruction. The pressure recover to a pressure level lower than the pressure before the obstruction and adds a head loss to the flow.
Equation (3) can be modified with diameters to:
q = cd (π / 4) D22 (2 (p1 - p2) / ρ (1 - d4))1/2 (4)
where
D2 = orifice, venturi or nozzle inside diameter (m, ft)
D1 = upstream and downstream pipe diameter (m, ft)
d = D2/ D1 diameter ratio
π = 3.14...
Equation (4) can be modified to mass flow for fluids by simply multiplying with the density:
m = cd (π / 4) D22 ρ ( 2 (p1 - p2) / ρ (1 - d4))1/2 (5)
where
m = mass flow (kg/s)
When measuring the mass flow in gases, its necessary to considerate the pressure reduction and change in density of the fluid. The formula above can be used with limitations for applications with relatively small changes in pressure and density.
The Orifice Plate
The orifice meter consists of a flat orifice plate with a circular hole drilled in it. There is a pressure tap upstream from the orifice plate and another just downstream. There are in general three methods for placing the taps. The coefficient of a meter depends on the position of the taps.
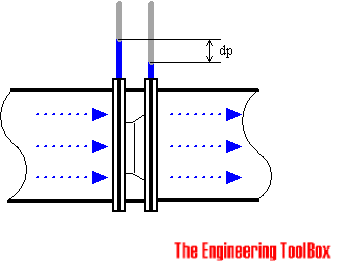
- Flange location - Pressure tap location 1 inch upstream and 1 inch downstream from face of orifice
- "Vena Contracta" location - Pressure tap location 1 pipe diameter (actual inside) upstream and 0.3 to 0.8 pipe diameter downstream from face of orifice
- Pipe location - Pressure tap location 2.5 times nominal pipe diameter upstream and 8 times nominal pipe diameter downstream from face of orifice
The discharge coefficient - cd - varies considerably with changes in area ratio and the Reynolds number. A discharge coefficient cd = 0.60 may be taken as standard, but the value varies noticeably at low values of the Reynolds number.
Diameter Ratio d = D2 / D1 | Discharge Coefficients - cd | |||
|---|---|---|---|---|
| Reynolds Number - Re | ||||
| 104 | 105 | 106 | 107 | |
| 0.2 | 0.60 | 0.595 | 0.594 | 0.594 |
| 0.4 | 0.61 | 0.603 | 0.598 | 0.598 |
| 0.5 | 0.62 | 0.608 | 0.603 | 0.603 |
| 0.6 | 0.63 | 0.61 | 0.608 | 0.608 |
| 0.7 | 0.64 | 0.614 | 0.609 | 0.609 |
The pressure recovery is limited for an orifice plate and the permanent pressure loss depends primarily on the area ratio. For an area ratio of 0.5 the head loss is about 70 - 75% of the orifice differential.
- The orifice meter is recommended for clean and dirty liquids and some slurry services.
- The rangeability is 4 to 1
- The pressure loss is medium
- Typical accuracy is 2 to 4% of full scale
- The required upstream diameter is 10 to 30
- The viscosity effect is high
- The relative cost is low
Example - Orifice Flow
An orifice with diameter D2 = 50 mm is inserted in a 4" Sch 40 steel pipe with inside diameter D1 = 102 mm. The diameter ratio can be calculated to
d = (50 mm) / (102 mm)
= 0.49
From the table above the discharge coefficient can be estimated to approximately 0.6 for a wide range of the Reynolds number.
If the fluid is water with density 1000 kg/m3 and the pressure difference over the orifice is 20 kPa (20000 Pa, N/m2) - the mass flow through the pipe can be calculated from (5) as
m = 0.6 (π / 4) (0.05 m)2 (1000 kg/m3) (2 (20000 Pa) / (1000 kg/m3) (1 - 0.494))1/2
= 7.7 kg/s
Orifice Calculator
The orifice calculator is based on eq. 5 and can be used to calculate mass flow through an orifice.
Typical Orifice Kv Values
| Orifice Diameter (mm) | Kv (m3/h) |
|---|---|
| 0.8 | 0.02 |
| 1.2 | 0.05 |
| 1.6 | 0.08 |
| 2.4 | 0.17 |
| 3.2 | 0.26 |
| 3.6 | 0.31 |
| 4.8 | 0.45 |
| 6.4 | 0.60 |
| 8 | 1.5 |
| 9 | 1.7 |
| 13 | 3 |
| 16 | 4 |
| 18 | 4.5 |
| 19 | 6.5 |
| 25 | 11 |
| 32 | 15 |
| 38 | 22 |
| 51 | 41 |
| 64 | 51 |
| 76 | 86 |
| 80 | 99 |
| 100 | 150 |
| 125 | 264 |
| 150 | 383 |
References
- American Society of Mechanical Engineers (ASME). 2001. Measurement of fluid flow using small bore precision orifice meters. ASME MFC-14M-2001.
- International Organization of Standards (ISO 5167-1:2003). Measurement of fluid flow by means of pressure differential devices, Part 1: Orifice plates, nozzles, and Venturi tubes inserted in circular cross-section conduits running full. Reference number: ISO 5167-1:2003.
- International Organization of Standards (ISO 5167-1) Amendment 1. 1998. Measurement of fluid flow by means of pressure differential devices, Part 1: Orifice plates, nozzles, and Venturi tubes inserted in circular cross-section conduits running full. Reference number: ISO 5167-1:1991/Amd.1:1998(E).
- American Society of Mechanical Engineers (ASME). B16.36 - 1996 - Orifice Flanges
The Venturi Meter
In the venturi meter the fluid is accelerated through a converging cone of angle 15-20o and the pressure difference between the upstream side of the cone and the throat is measured and provides a signal for the rate of flow.
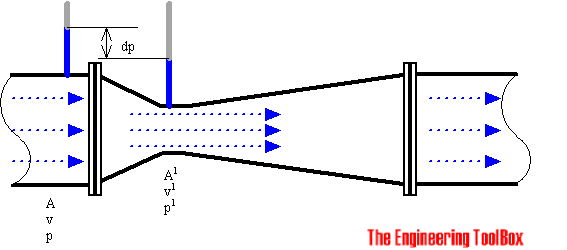
The fluid slows down in a cone with smaller angle (5 - 7o) where most of the kinetic energy is converted back to pressure energy. Because of the cone and the gradual reduction in the area there is no "Vena Contracta". The flow area is at a minimum at the throat.
High pressure and energy recovery makes the venturi meter suitable where only small pressure heads are available.
A discharge coefficient cd = 0.975 can be indicated as standard, but the value varies noticeably at low values of the Reynolds number.
The pressure recovery is much better for the venturi meter than for the orifice plate.
- The venturi tube is suitable for clean, dirty and viscous liquid and some slurry services.
- The rangeability is 4 to 1
- Pressure loss is low
- Typical accuracy is 1% of full range
- Required upstream pipe length 5 to 20 diameters
- Viscosity effect is high
- Relative cost is medium
References
- International Organization of Standards - ISO 5167-1:2003 Measurement of fluid flow by means of pressure differential devices, Part 1: Orifice plates, nozzles, and Venturi tubes inserted in circular cross-section conduits running full. Reference number: ISO 5167-1:2003.
- American Society of Mechanical Engineers ASME FED 01-Jan-1971. Fluid Meters Their Theory And Application- Sixth Edition
The Nozzle
Nozzles used for determining fluid's flowrate through pipes can be in three different types:
- The ISA 1932 nozzle - developed in 1932 by the International Organization for Standardization or ISO. The ISA 1932 nozzle is common outside USA.
- The long radius nozzle is a variation of the ISA 1932 nozzle.
- The venturi nozzle is a hybrid having a convergent section similar to the ISA 1932 nozzle and a divergent section similar to a venturi tube flowmeter.
Diameter Ratio d = D2/ D1 | Discharge Coefficient - cd | |||
|---|---|---|---|---|
| Reynolds Number - Re | ||||
| 104 | 105 | 106 | 107 | |
| 0.2 | 0.968 | 0.988 | 0.994 | 0.995 |
| 0.4 | 0.957 | 0.984 | 0.993 | 0.995 |
| 0.6 | 0.95 | 0.981 | 0.992 | 0.995 |
| 0.8 | 0.94 | 0.978 | 0.991 | 0.995 |
- The flow nozzle is recommended for both clean and dirty liquids
- The rangeability is 4 to 1
- The relative pressure loss is medium
- Typical accuracy is 1-2% of full range
- Required upstream pipe length is 10 to 30 diameters
- The viscosity effect high
- The relative cost is medium
References
- American Society of Mechanical Engineers ASME FED 01-Jan-1971. Fluid Meters Their Theory And Application- Sixth Edition
- International Organization of Standards - ISO 5167-1:2003 Measurement of fluid flow by means of pressure differential devices, Part 1: Orifice plates, nozzles, and Venturi tubes inserted in circular cross-section conduits running full. Reference number: ISO 5167-1:2003.
Example - Kerosene Flow Through a Venturi Meter
The pressure difference dp = p1 - p2 between upstream and downstream is 100 kPa (1×105 N/m2). The specific gravity of kerosene is 0.82.
Upstream diameter is 0.1 m and downstream diameter is 0.06 m.
Density of kerosene can be calculated as:
ρ = 0.82 (1000 kg/m3)
= 820 (kg/m3)
- Density, Specific Weight and Specific Gravity - An introduction and definition of density, specific weight and specific gravity. Formulas with examples.
Upstream and downstream area can be calculated as:
A1 = π ((0.1 m) / 2)2
= 0.00785 (m2)
A2 = π ((0.06 m) / 2)2
= 0.002826 (m2)
Theoretical flow can be calculated from (3):
q = A2 (2 (p1 - p2) / ρ (1 -(A2 / A1)2))1/2
q = (0.002826 m2) (2 (105 N/m2) / (820 kg/m3)(1 - ((0.002826 m2) / (0.00785 m2))2))1/2
= 0.047 (m3/s)
For a pressure difference of 1 kPa (0,01×105 N/m2) - the theoretical flow can be calculated:
q = (0.002826 m2) (2 (0.01×105 N/m2) / (820 kg/m3)(1 - ((0.002826 m2) / (0.00785 m2))2))1/2
= 0.0047 (m3/s)
The mass flow can be calculated as:
m = q ρ
= (0.0047 m3/s) (820 kg/m3)
= 3.85 (kg/s)
Flow Rate and Change in Pressure Difference
Note! - The flow rate varies with the square root of the pressure difference.
From the example above:
- a tenfold increase in the flow rate requires a one hundredfold increase in the pressure difference!
Transmitters and Control System
The nonlinear relationship have impact on the pressure transmitters operating range and requires that the electronic pressure transmitters have the capability to linearizing the signal before transmitting it to the control system.
Accuracy
Due to the non linearity the turn down rate is limited. The accuracy strongly increases in the lower part of the operating range.
- More about Flow Meters as Orifices, Venturi meters, and Nozzles
- Fluid Mechanics
- The Bernoulli Equation
- The Continuity Equation
- TurnDown Ratio and Flow Measurement Devices - An introduction to Turn Down Ratio and flow measurement accuracy.



