Velocity-Area Flowmetering
Flow rate or discharge in an open conduit, channel or river can be calculated with the velocity-area principle.
The velocity-area principle is based on velocity measurements in a open flow like a conduit, channel or river.
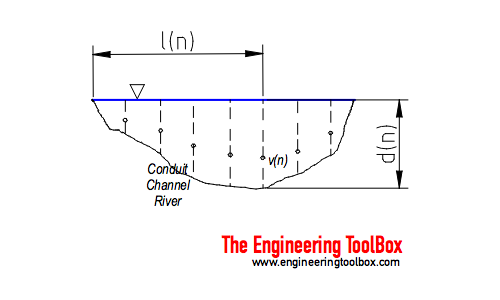
Velocities and depths across the stream are measured as indicated in the figure above. A partial discharge in a section of the stream can be calculated as
qn = vn an (1)
where
qn = flow rate or discharge in section n (m3/s, ft3/s)
vn = measured velocity in section n (m/s, ft/s)
an = area of section n (m2, ft2)
One simple way to express the section area is
an = dn (ln+1 - ln-1) / 2 (2)
The total flow in the stream can be summarized to
Q = Σ1n vn an (3)
where
Q = summarized flow rate or discharge in the conduit (m3/s, ft3/s)
The accuracy of estimate depends on the profile of the conduit and the number of measurements. For conduits with regular shapes like rectangular channels a limited number of measurements are required. For irregular shapes - like natural rivers or similar - higher accuracy requires more measurements both horizontal and vertical.
Example - Computing Flow Rate in a Channel
From a conduit we have three measurements:
| Measured Values | Calculated Values | ||||
|---|---|---|---|---|---|
| n | v (m/s) | d (m) | l (m) | a (m2) | q (m3/s) |
| 0 | 0 | 0 | 0 | ||
| 1 | 3 | 1 | 2 | 2 | 6 |
| 2 | 4 | 1.5 | 4 | 3 | 12 |
| 3 | 3 | 0.9 | 6 | 1.8 | 5.4 |
| 4 | 0 | 0 | 8 | ||
| Summarized | 23.4 | ||||
The section areas can be calculated like
a1 = (1 m) ((4 m) - (0 m)) / 2
= 2 m2
a2 = (1.5 m) ((6 m) - (2 m)) / 2
= 3 m2
a3 = (0.9 m) ((8 m) - (4 m)) / 2
= 1.8 m2
The flow rates can be calculated as
q1 = (3 m/s) (2 m2)
= 6 m3/s
q2 = (4 m/s) (3 m2)
= 12 m3/s
q3 = (3 m/s) (1.8 m2)
= 5.4 m3/s
The total flow can be summarized as
Q = (6 m3/s) + (12 m3/s) + (5.4 m3/s)
= 23.4 m3/s
Note - there are alternative ways to calculate the section flow rates:
Simple Average Method
Using the simple average of two successive vertical depths, their mean velocity, and the distance between them can be expressed as
qn to n+1 = [(vn + vn+1) / 2] [(dn + dn+1 ) / 2] (ln+1 - ln) (4)
Midsection Method
With the midsection method, the depth and mean velocity are measured for each number of verticals along the cross section. The depth at a vertical is multiplied by the width, which extends halfway to the preceding vertical and halfway to the following vertical, to develop a cross-sectional area. The section flow rate can be expressed as
qn = vn [((ln - ln-1) + (ln+1 - ln)) / 2] dn (5)
Related Topics
-
Flow Measurements
Flow metering principles - Orifice, Venturi, Flow Nozzles, Pitot Tubes, Target, Variable Area, Positive Displacement, Turbine, Vortex, Electromagnetic, Ultrasonic Doppler, Ultrasonic Time-of-travel, Mass Coriolis, Mass Thermal, Weir V-notch, Flume Parshall and Sluice Gate flow meters and more.
Related Documents
-
Comparing Flowmeters
A limited comparison of flowmeter principles - regarding service, rangeability, pressure loss, typical accuracy, upstream pipe diameters, viscosity and relative costs. -
Flowmeter - Accuracy
Introduction to accuracy in flow measurement devices. -
Flowmeters - Turndown Ratios
Turndown ratio (Rangeability) can be used to compare flow measurement devices like orifices, venturi meters etc. -
Fluid Flowmeters - Comparing Types
An introduction to the different types of fluid flowmeters - Orifices, Venturies, Nozzles, Rotameters, Pitot Tubes, Calorimetrics, Turbine, Vortex, Electromagnetic, Doppler, Ultrasonic, Thermal, Coriolis. -
Hydrostatic Pressure vs. Depth
Depth and hydrostatic pressure. -
Open Channel Weirs - Volume Flow Measurements
Weirs can be used to measure flow rates in open channels and rivers - common for water supply and sewage plants. -
Orifice, Nozzle and Venturi Flow Rate Meters
The orifice, nozzle and venturi flow rate meters makes the use of the Bernoulli Equation to calculate fluid flow rate using pressure difference through obstructions in the flow. -
Sluice Gate - Volume Flow Measurements
Sluice gates can be used to control and measure volume flow rates in open channels and rivers, mainly in connection to hydro power plants. -
U-Tube Differential Pressure Manometers
Inclined and vertical u-tube manometers used to measure differential pressure in flow meters like pitot tubes, orifices and nozzles. -
Velocity Pressure Head
Dynamic pressure or velocity head. -
Volume Flow - Online Unit Converter
Convert between volume flow units like gpm, liter/sec, cfm, m3/h. -
Water - Volume Flow Measurement
A manual providing guidance in selecting, managing, inspecting, and maintaining water measurement devices - describes standard methods and devices commonly used to measure irrigation water.




