WABT - Weighted Average Bed Temperature

Definition and examples of calculation of weighted average bed temperature in adiabatic reactors.

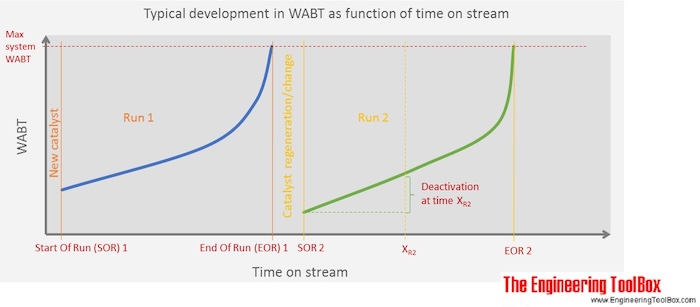
WABT - Weighted Average Bed Temperature is a way to get one representative temperature from an adiabatic reactor (no heat loss or gain to the surroundings), which in reality have an increasing or decreasing temperature profile from inlet to outlet. The temperature profile occurs due to exothermic or endothermic reactions taking place in the reactor. The WABT is used to indicate the catalyst activity in catalytic processes, where a deactivation of the catalyst starts to take place from the start-up after a catalyst change. To maintain the catalyst activity despite the deactivation, the inlet temperature is gradually increased by the operators and the temperature profile through the reactor changes over time. WABT at start of a run is compared to WABT at a given time after start-up, and the difference is telling something about the degree of catalyst deactivation.

WABT_with_TOS

WABT is the average temperature of each catalytic bed between two temperatur indicators, and Tⁱⁿ and T^out are the inlet and outlet temperatures in each catalytic bed, respectively. The global WABT is calculated with

WABT

where

N = the number of catalyst beds
Wc_i = the weight fraction of catalyst in each bed with respect to the total

In real life the number of temperatur indicators may be limited to one at the inlet and one at the outlet, only. Other places there might be a lot of thermocouples throughout the reactor, both in radial and length direction. Below, examples of calculation of WABT in different cases are given.

Example 1: One reactor and two thermocouples

WABT_simple case
In this case both N and Wc_i are 1, and Tⁱⁿ = T₁ and T^out = T₂

WABT = (T₁ + 2*T₂)/3 * 1

If T₁=350 °C and T₂=395°C,

WABT = (350°C + 2*395°C)/3 = 380°C

Example 2: Three reactors and Tⁱⁿ and T^out of each reactor

WABT_3_reactors
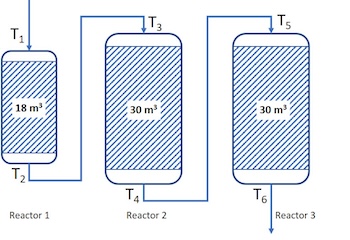
T₁=345°C, T₂=380°C, T₃=370°C, T₄=390°C, T₅=385°C and T₆=395°C

In this case we have temperature indicators, but we must also know the bulk density of the catalyst beds to do the right weighting of the temperature.

Lets say that the catalyst bulk dencities ρ1= 550 kg/m³, ρ2= 800 kg/m³ and ρ3=750 kg/m³are for catalyst beds in reactor 1, 2 and 3, respectively. Then, first we calculate weight fraction the total catalyst mass in each reactor:

Catalyst weight in R1: 18 [m³]*550[kg/m³] = 9 900 [kg]
Catalyst weight in R2: 30 [m³]*800[kg/m³] = 24 000 [kg]
Catalyst weight in R3: 30 [m³]*750[kg/m³] = 22 500 [kg]
Total catalyst weight: 56 400 [kg]

Wc_R1 = 9900/56400 = 0.18
Wc_R2 = 24000/56400 = 0.42
Wc_R3 = 22500/56400 = 0.40

Then, we can calculate the WABT:

WABT = WABT_R1*Wc_R1 + WABT_R2*Wc_R2 + WABT_R3*Wc_R3

= (T₁+2T₂)/3*0.18 + (T₃+2T₄)/3*0.42 + (T₅+2T₆)/3*0.40

= (345 + 2*380)/3*0.18 + (370 + 2*390)/3*0.42 + (385 + 2*395)/3*0.40 = 384°C

Example 3: One reactor with two chains of thermocouples throughout the reactor

WABT_1_reactor
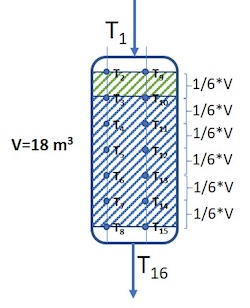
T₁=351°C, T₂=350°C, T₃=368°C, T₄=386°C, T₅=399°C, T₆=406°C, T₇=411°C, T₈=413°C, T₉=350°C, T₁₀=370°C, T₁₁=387°C, T₁₂=398°C, T₁₃=405°C, T₁₄=410°C, T₁₅=412°C and T₁₆=411°C

In this case there is a 1/6 top layer of catalyst, with density ρ1= 550 kg/m³, while the rest of the catalyst mass (5/6) has density ρ2= 800 kg/m³. Then the catalyst weight fractions for each of the fractions of the catalyst bed will be:

Catalyst weight top layer: 18*1/6 [m3] * 550 [kg/m3] = 1 650 [kg]
Catalyst weight layer 2 to 6: 18*1/6 [m3] * 800 [kg/m3] = 2 400 [kg]
Total catalyst weight: 1 650 [kg] + 2 400[kg]*5 = 13 650 [kg]

Wc₁ = 1650/13650= 0.12
Wc₂ = Wc₃ = Wc₄ = Wc₅ = Wc₆ = 2400/13650 = 0.176

WABT = WABT₁*Wc₁ + WABT₂*Wc₂ + WABT₃*Wc₃+ WABT₄*Wc₄ + WABT₅*Wc₅ + WABT₆*Wc₆

= WABT₁*Wc₁ + Wc₂*(WABT₂+ WABT₃ + WABT₄ + WABT₅ + WABT₆)

In this case, there are two thermocouples at each height level in the reactor, and Tⁱⁿ and T^out of each fraction is the average of these two. Then, WABT is:

WABT = ((T₂+T₉)/2+2*(T₃+T₁₀)/2)/3*0.12 + 0.176*(((T₃+T₁₀)/2+2*(T₄+T₁₁)/2)/3 + ((T₄+T₁₁)/2+2*(T₅+T₁₂)/2)/3 + ((T₅+T₁₂)/2+2*(T₆+T₁₃)/2)/3 + ((T₆+T₁₃)/2+2*(T₇+T₁₄)/2)/3 + ((T₇+T₁₄)/2+2*(T₈+T₁₅)/2)/3)

= ((350+350)/2+2*(368+370)/2)/3*0.12 + 0.176*(((368+370)/2+2*(386+387)/2)/3 + ((386+387)/2+2*(399+398)/2)/3 + ((399+398)/2+2*(406+405)/2)/3 + ((406+405)/2+2*(411+410)/2)/3 + ((411+410)/2+2*(413+412)/2)/3 = 395.3°C

It should be obvious that this is a more precise measurement/calculation than the more simple

WABT = (T₁ + 2*T₁₆)/3 * 1

= (351 + 2*411)/3*1 = 391.0 °C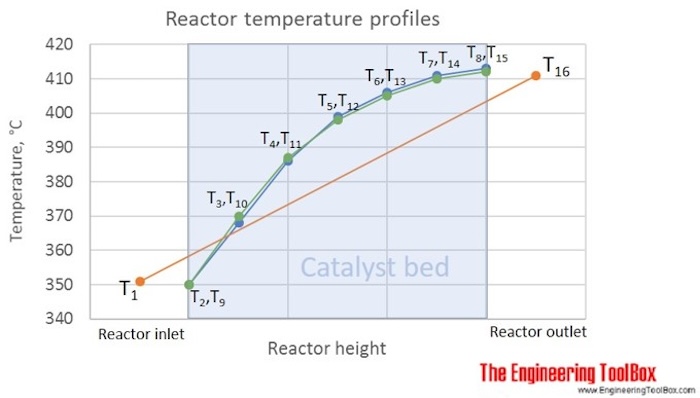

reactor_temperature_profile

The figure above shows the given temperature profile, which is typical for a gas oil hydrotreater in a refinery. Calculating WABT from T₁ and T₁₆, only, gives 391°C, while using the catalyst bed temperatures, measured by T₂ to T₁₅, gives WABT = 395°C. If calculating the average bed temperature, simply as the average of T₁ and T₁₆, you get 381°C, which is much less representative for the temperature in the catalyst bed than the WABT using the same temperatures.

The reason for the actual shape given in this figure, is that the fastest reactions, in this case, are the most exothermic (giving a fast temperature increase at the reactor inlet), and when their potential is used up (reach equilibrium or reactants are consumed), more slow, and less exothermic reactions take place.