Hydrocarbon Mixtures - Molecular Weight vs. Gravity and Average Boiling Point

Formulas and examples of calculation of average molecular weight of hydrocarbon mixtures from gravity and average boiling point, achieved from distillation data.

Sponsored Links

For many purposes in chemical engineering, there is important to know the molecular weight (MW) of the fluids in process streams, and for mixtures of several different compounds an average molecular weight can be useful. But, exact analysis of the composition of complex mixtures of hydrocarbons, such as crude oil or oil distillation fractions, which can consist of several thousand different compounds, is difficult to get. Direct measurement of molecular weight is time demanding and gives imprecise results. However, there are several models calculating average molecular weight, based on gravity and distillation data. Two of the most used models, recommended by API, are given below:

Riazi-Daubert 1980: MW = 4.5673E-05 _* T_R^2.1962_* S^-1.0164 (1)

or MW = 1.6607E-04 _* T_K^2.1962_* S^-1.0164 (2)

Riazi-Daubert extended: MW = 20.486 _*T_R^1.26007_*S^4.98308_*e^{(1.165E-04*T_R -7.78712*S +1.1582E-03*T_R*S)} (3)

or MW = 42.965 _*T_K^1.26007_*S^4.98308_*e^{(2.097E-04*T_K-7.78712*S+2.08476E-03*T_K*S)} (4)

Where

T_R = MeABP (mean average boiling point), in °R (degree Rankin)
T_K = MeABP (mean average boiling point), in K (degree Kelvin)
S = Specific gravity at 60 °F (= 15.6°C)

Equation (1) and (2) fail to properly predict properties for hydrocarbons above C₂₅, with boiling point > 400°C (750°F). For heavier oil samples equation (3) and (4) are recommended. These relationships are valid in the ranges:

Molweight: 70 to 700 kg/kmol
MeABP: 20 - 560°C (90 to 1050 °F)
API: 14° to 93°
Specific gravity: 0.630 to 0.973

The average error is said to be about 7%.
Eq. (2) and (4) are used to calculate the molecular weight for a number of specific gravities and boiling points and the results, given with °C and °F, are shown in the figures below

molecular_weight_gravity_boiling_point

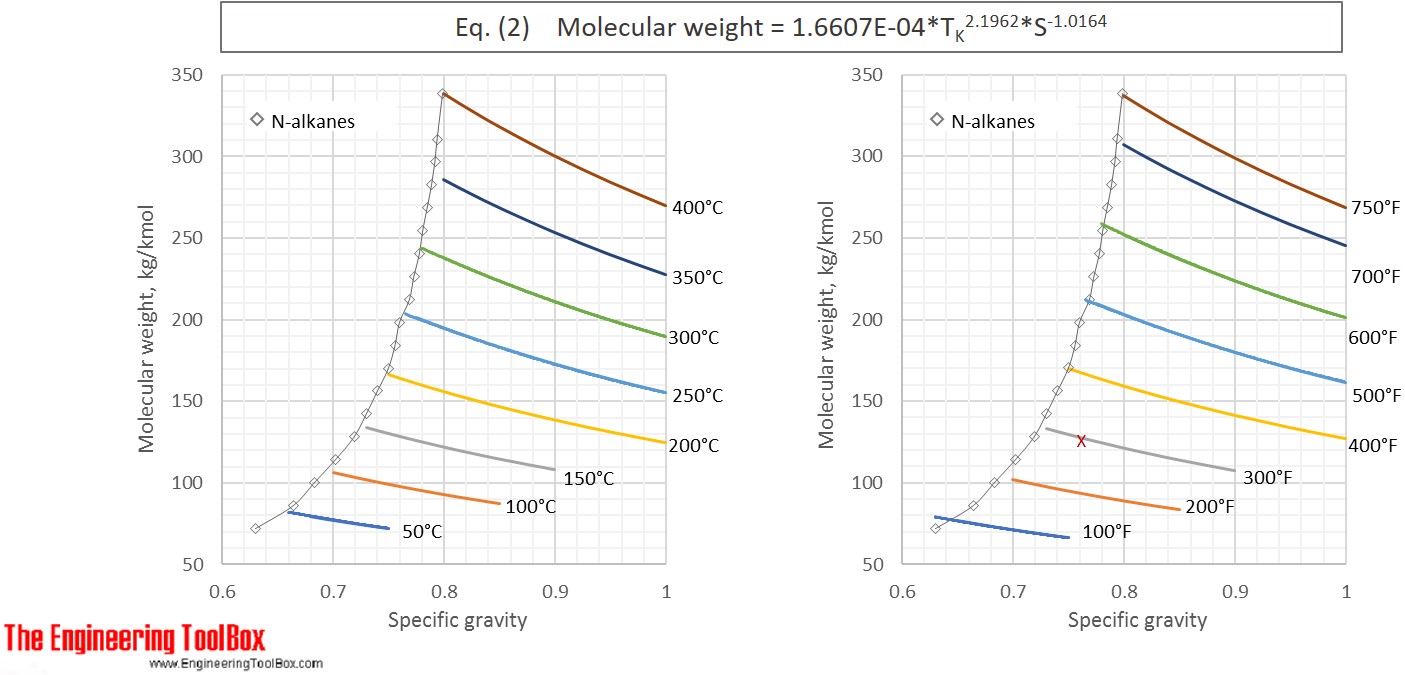
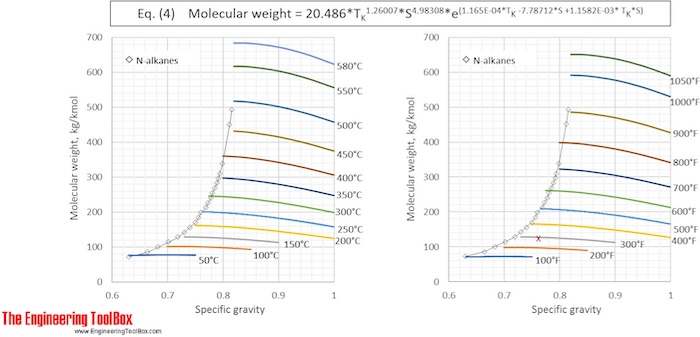
See also Average boiling point from gravity and molecular weight and Molecular Weight - Gases and Vapors

Example 1: Molecular weight of naphtha
Calculate the molecular weight of a naphtha with specific gravtity, S = 0.763 and a MeABP of 292°F

Naphtha is in the low boiling point range, and equation (1) can be applied.

First, °F are converted to °R:
MeABP = 292°F + 460 = 752°R

Average MW = 4.5673E-05 _* 752^2.1962_* 0.763^-1.0164 = 124.6 kg/kmol

Applying equation (3) gives

Average MW = 20.486_*752^1.26007_*0.763^4.98308_*e^{(1.165E-04*752 -7.78712*0.763 +1.1582E-03*752*0.763)} = 124.8 kg/kmol

The results from Example 1 are given as a red X in the figures. The difference between molecular weight of naphtha from Eq (1) and (3) is 0.2 %.

Example 2: Molecular weight of a light gas oil from a distillation curve

D86 used to distille a gas oil sample showes:
10vol% recovered at 255 °C
30vol% recovered at 280 °C
50vol% recovered at 303 °C
70vol% recovered at 325 °C
90vol% recovered at 351 °C

The sample gravity is measured to be of 31.4°API

First, API gravity must be converted to specific gravity:
S, specific gravity = 141.5/(31.4°API +131.5) = 0.869

Then, VABP (volume average boiling point) and the distillation curve slope is calculated:
VABP = 0.2*(255+280+303+325+351) = 303 °C.
Slope = (351-255)/80 = 1.2 °C/% recovered.

MeABP can then be found by using correction factors:
MeABP = VABP + (-5)°C = 303-5 = 298°C
°C is then converted to K : MeABP = 298°C + 273 = 571 K

Finally, by applying equation (2) the molweight can be calculated:

Average MW = 1.6607E-04 _* 571^2.1962 * 0.869^-1.0164 = 217 kg/kmol

Applying equation (4) gives

Average MW = 42.965_*571^1.26007_*0.869^4.98308_*e^{(2.097E-04*571-7.78712*0.869+2.08476E-03*571*0,869)} = 232 kg/kmol

The difference between MW of gas oil from Eq (2) and (4) is 6.5 %.