Hydrocarbon Mixtures - Average Boiling Points vs. Gravity and Molecular Weights
Formulas and examples of calculation of boiling point of hydrocarbon mixtures from gravity and molecular weight.
Boiling point: The temperature at which a liquid turns into a gas
For many purposes in chemical engineering, there is important to know the boiling point of the fluids in process streams. When the fluid consists of a mixture of many different compounds, the average boiling point (ABP) can be useful. But boiling point information from real distillation or gas chromatographic analysis is not always available. However, there are several models calculating average boiling point, based on other properties of the fluid. For hydrocarbons, such as crude oil and distillation fractions of crude oil, the best input pair of parameters to predict boiling point is molecular weight and specific gravity. Two correlations based on these from Riazi-Daubert are given below:
Riazi-Daubert, for molecular weights of 70-300: Tb = 3.76587*e(3.7741E-03*M+2.98404*S-4.25288E-03*M*S)*M0.40167*S-1.58262 (1)
Riazi-Daubert, for molecular weights of 300-700: Tb = 9.3369*e(1.6514E-04*M+1.4103*S-7.5152E-04*M*S)*M0.5369*S-0.7276 (2)
Eq. (2) is also applicable to hydrocarbons having molecular weight range of 70-300, but with less accuracy
Where
Tb = Average boiling point, in Kelvin
M = Average molecular weight
S = Specific gravity at 60 °F (= 15.6°C)
See also Molecular weight from average boiling point and gravity
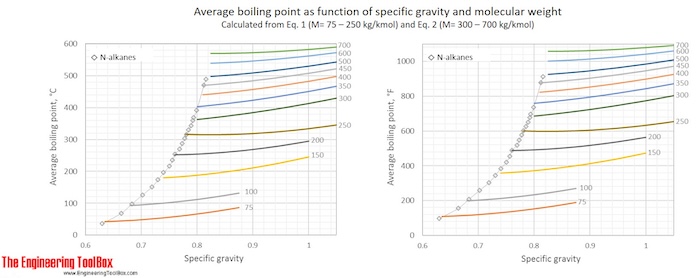
Eq. (1) and (2) are used to calculate Tb for a number of specific gravities and molecular weights and the results, in °C and °F, are given in the figures below.
Example 1: Average boiling point of naphtha
Calculate the average boiling point of a naphtha with specific gravtity, S = 0.763 and a molecular weight of 125.
Naphtha is in the low molecular weight range, and equation (1) should be applied.
ABP = 3.76587*e(3.7741E-03*125+2.98404*0.763-4.25288E-03*125*0.763)*1250.40167*0.763-1.58262 = 418 K
Converted to °C and °F: 418 K = 145°C = 293 °F
Applying equation (2) gives
ABP = 9.3369*e(1.6514E-04*125+1.4103*0.763-7.5152E-04*125*0.763)*1250.5369*0.763-0.7276 = 423 K = 150°C = 302°F
NB! For low molecular weights (< 300) this ABP is consider to be less accurate than calculated from Eq. (1).
Example 2: Average boiling point of a vacuum gas oil.
Calculate the average boiling point of a vacuum gas oil of gravity of 16.7°API and an average molecular weight of 391.
The vacuum gas oil has a molecular weight > 300, and Eq. (2) must be applied.
But first, we have to convert the API gravity to specific gravity:
S, specific gravity = 141.5/(16.7°API +131.5) = 0.955
ABP = 9.3369*e(1.6514E-04*391+1.4103*0.955-7.5152E-04*391*0.955)*3910.5369*0.955-0.7276 = 737 K = 464°C = 867°F
