Electrical Formulas

Common electrical units used in formulas and equations are:

• Volt - unit of electrical potential or motive force - potential is required to send one ampere of current through one ohm of resistance
• Ohm - unit of resistance - one ohm is the resistance offered to the passage of one ampere when impelled by one volt
• Ampere - units of current - one ampere is the current which one volt can send through a resistance of one ohm
• Watt - unit of electrical energy or power - one watt is the product of one ampere and one volt - one ampere of current flowing under the force of one volt gives one watt of energy
• Volt Ampere - product of volts and amperes as shown by a voltmeter and ammeter - in direct current systems the volt ampere is the same as watts or the energy delivered - in alternating current systems - the volts and amperes may or may not be 100% synchronous - when synchronous the volt amperes equals the watts on a wattmeter - when not synchronous volt amperes exceed watts - reactive power
• kiloVolt Ampere - one kilovolt ampere - kVA - is equal to 1000 volt amperes
• Power Factor - ratio of watts to volt amperes

Ohm's Law Calculator

Add values for two parameters and the two others will be calculated. Delete the input for the values you want to calculate.

I - Current (A)

R - Resistance (Ohm)

U - Voltage (V)

P - Power (W)

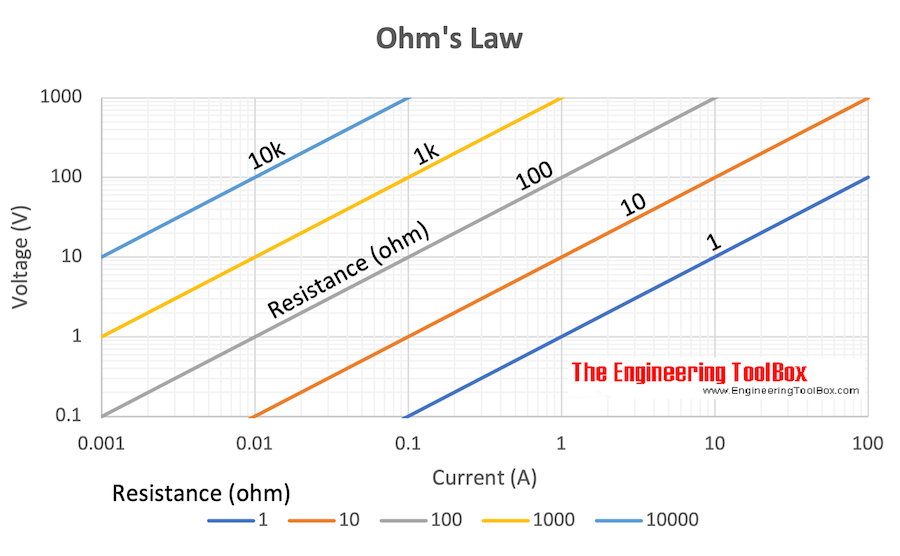
Electrical Potential - Ohm's Law

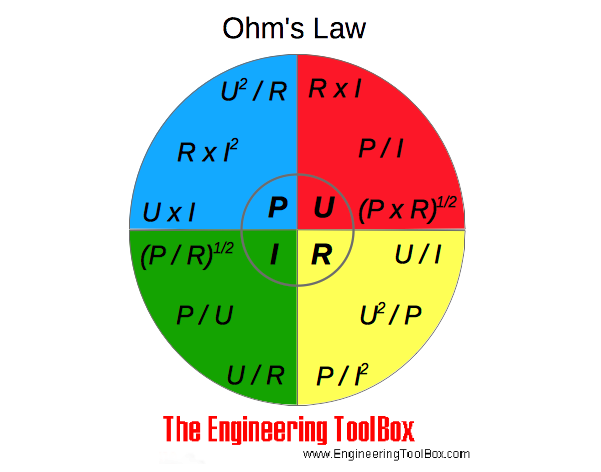
Ohm's law can be expressed as:

U = R I                        (1a)

U = P / I                      (1b)

U = (P R)^1/2                (1c)

Download and print Ohm's Law

Electric Current - Ohm's Law

I = U / R                      (2a)

I = P / U                      (2b)

I = (P / R)^1/2               (2c)

Electric Resistance - Ohm's Law

R = U / I                     (3a)

R = U² / P                    (3b)

R = P / I²                    (3c)

Example - Ohm's law

A 12 volt battery supplies power to a resistance of 18 ohms.

I = (12 V) / (18 Ω)

    = 0.67 (A)

• download Ohm's law as pdf-file

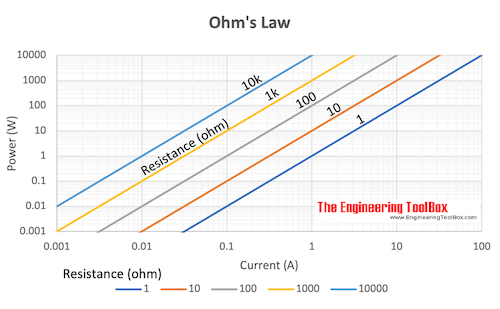
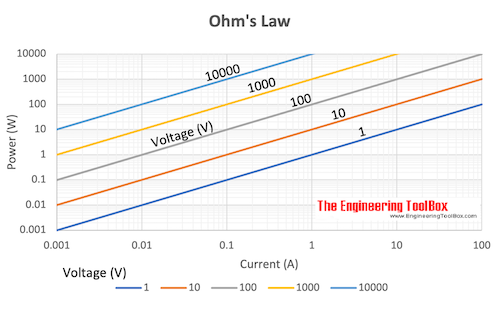
Electric Power

P = U I                      (4a)

P = R I²                    (4b)

P = U² / R                  (4c)

where

P = power (watts, W, J/s)

U = voltage (volts, V)

I = current (amperes, A)

R = resistance (ohms, Ω)

Download and print Ohm's Law

Download and print Ohm's Law

Electric Energy

Electric energy is power multiplied with time:

W = P t                       (5)

where

W = energy (Ws, J)

t = time (s)

Alternative - power can be expressed

P = W / t                     (5b)

Power is consumption of energy by consumption of time.

Example - Energy lost in a Resistor

A 12 V battery is connected in series with a resistance of 50 ohm. The power consumed in the resistor can be calculated as

P = (12 V)² / (50 ohm)

   = 2.9 W

The current through the resistor can be calculated as

I = (2.9 W) / (12 V)

  = 0.24 A

The energy dissipated in 60 seconds can be calculated

W = (2.9 W) (60 s)

  = 174 Ws, J

  = 0.174 kWs

  = 4.8×10^-5 kWh

Example - Electric Stove

An electric stove consumes 5 MJ of energy from a 230 V power supply when turned on in 60 minutes.

• energy to heat water

The power rating - energy per unit time - of the stove can be calculated as

P = (5 MJ) (10⁶ J/MJ) / ((60 min) (60 s/min))

   = 1389 W

   = 1.39 kW

The current can be calculated

I = (1389 W) / (230 V)

  = 6 ampere

Electrical Motors

Electrical Motor Efficiency

μ = 746 P_hp / P_{input_w}                 (6)

where

μ = efficiency

P_hp = output horsepower (hp)

P_{input_w} = input electrical power (watts)

or alternatively

μ = 746 P_hp / (1.732 V I PF)                      (6b)

Electrical Motor - Power

P_3-phase = (U I PF 1.732) / 1,000                    (7)

where

P_3-phase = electrical power 3-phase motor (kW)

PF = power factor electrical motor

Electrical Motor - Amps

I_3-phase = (746 P_hp) / (1.732 VμPF)                  (8)

where

I_3-phase = electrical current 3-phase motor (amps)

PF = power factor electrical motor