Steam Entropy
Basic steam thermodynamics - entropy diagram.
The entropy diagram for steam shows the relationships between
- Pressure
- Temperature
- Dryness Fraction
- Entropy
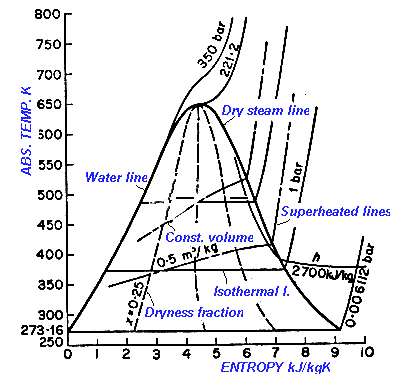
With two factors given - the others can be found in the diagram. The ordinates in the diagram represents the Entropy and the Absolute temperature.
The diagram consist of the following lines
- Isothermal line
- Pressure lines
- Lines of dryness fraction
- Waterline between water and steam
- Dry steam lines
- Constant volume lines
The total heat is given by the area enclosed by absolute zero base water line and horizontal and vertical line from the respective points.
An adiabatic expansion is a vertical line. An adiabatic process is expansion at constant entropy with no transfer of heat.
- Critical temperature of steam is 375 to 3,380oC
- Critical pressure is 217.8 atm
Total Entropy of Steam
Entropy of Water
The change of entropy can be expressed as:
dS = loge(T1/T) (1)
where
T = absolute temperature (K)
The entropy of water above freezing point can be expressed as:
dS = loge(T1/273) (2)
Entropy of Evaporation
Change of Entropy during evaporation
dS = dL/T (3)
where
L = latent heat (J)
Entropy of wet steam
The entropy of wet steam can be expresses as:
dS = loge(T1/273) +ζ(L1/T1) (4)
where
ζ = dryness fraction
Entropy of superheated steam
Change of entropy during super-heating can be expressed as
dS = cp loge( T/T1 ) (5)
where
cp= specific heat capacity at constant pressure for steam (kJ/kgK)
The entropy of superheated steam can be expressed as:
dS = loge( T1/273 ) + L1/T1 + cp loge( Ts/T1 ) (6)
where
Ts = absolute temperature of superheated steam
T1 = absolute temperature of evaporation
Water and Steam Entropy - Imperial Units
| Temperature (oF) | Absolute Pressure (psia) | Entropy (Btu/lb oF) | |
|---|---|---|---|
| Water | Steam | ||
| 0 | 0.0185 | -0.3243 | 2.330 |
| 10 | 0.0309 | -0.3141 | 2.283 |
| 20 | 0.0505 | -0.3038 | 2.238 |
| 30 | 0.0809 | -0.2936 | 2.195 |
| 32 (0 oC) | 0.0887 | 0.0000 | 2.187 |
| 40 | 0.1217 | 0.0162 | 2.159 |
| 50 | 0.1718 | 0.0361 | 2.126 |
| 60 | 0.2564 | 0.0555 | 2.094 |
| 70 | 0.3633 | 0.0746 | 2.064 |
| 80 | 0.5074 | 0.0933 | 2.035 |
| 90 | 0.6989 | 0.1116 | 2.008 |
| 100 | 0.9503 | 0.1296 | 1.982 |
| 110 | 1.277 | 0.1473 | 1.957 |
| 120 | 1.695 | 0.1647 | 1.933 |
| 130 | 2.226 | 0.1817 | 1.911 |
| 140 | 2.893 | 0.1985 | 1.889 |
| 150 | 3.723 | 0.2151 | 1.868 |
| 160 | 4.747 | 0.2314 | 1.848 |
| 170 | 5.999 | 0.2474 | 1.829 |
| 180 | 7.519 | 0.2632 | 1.811 |
| 190 | 9.350 | 0.2787 | 1.793 |
| 200 | 11.54 | 0.2941 | 1.776 |
| 210 | 14.12 | 0.3092 | 1.760 |
| 212 (100 oC) | 14.70 | 0.3122 | 1.756 |
| 220 | 17.20 | 0.3241 | 1.744 |
| 230 | 20.80 | 0.3389 | 1.729 |
| 240 | 24.99 | 0.3534 | 1.714 |
| 250 | 29.85 | 0.3678 | 1.700 |
- 1 psi (lb/in2) = 6894.8 Pa (N/m2)
- 1 Btu/(lbm oF) = 4186.8 J/ (kg K)
Related Topics
-
Thermodynamics
Thermodynamics of steam and condensate systems.
Related Documents
-
2nd Law of Thermodynamics
Entropy and disorder. -
Adiabatic Flame Temperatures
Adiabatic flame temperatures for hydrogen, methane, propane and octane - in Kelvin. -
Compressible Gas Flow - Entropy
Calculating the entropy in a compressible gas flow. -
Properties of Saturated Steam - SI Units
Saturated Steam Table with steam properties as specific volume, density, specific enthalpy and specific entropy. -
Saturated Steam - Properties - Imperial Units
Steam table with sensible, latent and total heat, and specific volume at different gauge pressures and temperatures. -
Saturated Steam - Properties for Pressure in Bar
Saturated Steam Table with properties like boiling point, specific volume, density, specific enthalpy, specific heat and latent heat of vaporization. -
Standardized Enthalpies and Entropies
Standardized enthalpies and entropies for some common substances. -
Steam and Vapor Enthalpy
Vapor and steam enthalpy, specific enthalpy of saturated liquid, saturated vapor and superheated vapor. -
Superheated Steam - Entropy
The entropy of steam superheated to temperatures above saturation points. -
Third Law of Thermodynamics
The entropy of a substance is zero if the absolute temperature is zero. -
Water - Thermophysical Properties
Thermal properties of water at different temperatures like density, freezing temperature, boiling temperature, latent heat of melting, latent heat of evaporation, critical temperature and more. -
Water-Steam Mollier Diagram
Enthalpy-entropy diagram for water and steam. -
Wet Steam - Enthalpy
Wet steam, dryness fraction and enthalpy. -
Wet Steam - Specific Volume
Wet steam and specific volume.
