Projectile Range
Calculate the range of a projectile - a motion in two dimensions.
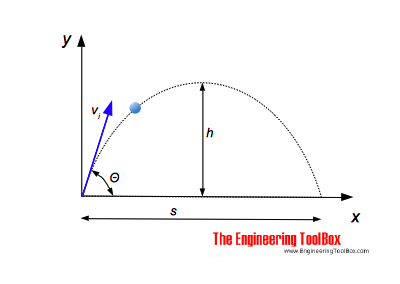
The time for a projectile - a bullet, a ball or a stone or something similar - thrown out with an angle Θ to the horizontal plane - to reach the maximum height can be calculated as
th = vi sin(Θ) / ag (1)
where
th = time to reach maximum height (s)
vi = initial velocity of the projectile (m/s, ft/s)
Θ = the initial angle of the velocity vector to the horizontal plane (degrees)
ag = acceleration of gravity (9.81 m/s2, 32.174 ft/s2)
The total flight time can be expressed as
ts = 2 th
= 2 vi sin(Θ) / ag (2)
where
ts = time for the total flight (s)
The maximum elevation - h - of the flight can be calculated as
h = 1/2 ag th 2 (3)
where
h = flight maximum elevation (m, ft)
The horizontal distance of the flight can be expressed as
s = vi2 sin(2 Θ) / ag (4)
where
s = flight distance (m, ft)
Example - Throwing a Ball
A ball is thrown with initial velocity 25 m/s in angle 30 degrees to the horizontal plane. The time for the ball to reach maximum level is
th = (25 m/s) sin(30 degrees) / (9.81 m/s2)
= 1.27 s
The maximum elevation of the ball can be calculated as
h = 1/2 (9.81 m/s2) (1.27 s)2
= 7.91 m
The horizontal distance traveled by the ball can be calculated as
s = ( 25 m/s)2 sin(2 30 degrees) / (9.81 m/s2)
= 55.2 m
Projectile Flight Calculator
The calculator below can be used to estimate the time of flight, time to reach maximum elevation, maximum elevation and flight distance for a projectile like a bullet or a ball or something similar.
Note that friction force due to air resistance is neglected.
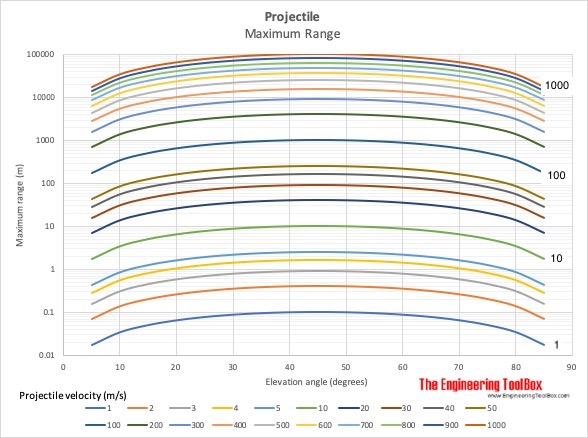
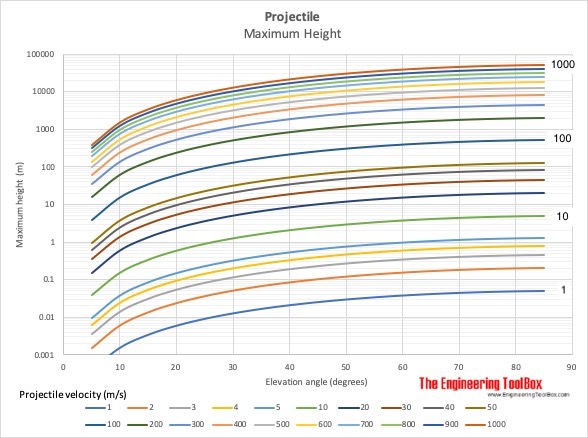
Note that friction force due to air resistance is neglected in the charts above. For higher velocities range and maximum height will be dramatically reduced.



