Piping Elbows - Thrust Block Forces
Thrust block forces on pipe bends anchors due to liquid velocities and internal pressures - online resulting force calculator.
In a piping structure without adequately support fluid flow and internal pressure may create intolerable forces and tensions.
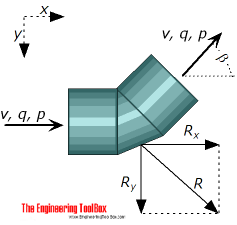
The resultant force - or required support force - on a thrust block - or an anchor - for a bend depends on
- the fluid mass flow, or flow velocity
- the change of flow direction
- the internal pressure
With no flow and no pressure there is no force.
Online Pipe Bend Resulting Force Calculator
The calculator below can used to calculate the resulting force in a piping bend:
Resulting force due to Mass flow and Flow Velocity
The resulting force in x-direction due to mass flow and flow velocity can be expressed as:
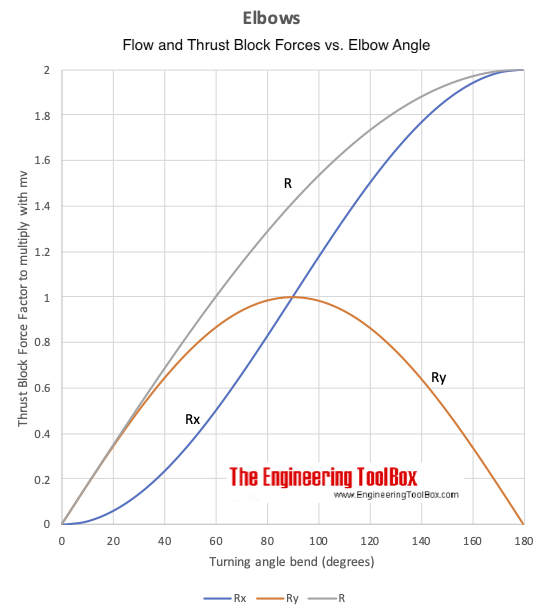
Rx = m v (1 - cos(β)) (1)
= ρ A v2 (1 - cos(β)) (1b)
= ρ π (d / 2)2 v2 (1 - cos(β)) (1c)
where
Rx = resulting force in x-direction (N)
m = mass flow (kg/s)
v = flow velocity (m/s)
β = turning bend angle (degrees)
ρ = fluid density (kg/m3)
d = internal pipe or bend diameter (m)
π = 3.14...
The resulting force in y-direction due to mass flow and flow velocity can be expressed as:
Ry = m v sin(β) (2)
= ρ A v2 sin(β) (2b)
= ρ π (d / 2)2 v2 sin(β) (2c)
Ry = resulting force in y direction (N)
The resulting force on the bend due to force in x- and y-direction can be expressed as:
R = (Rx2 + Ry2)1/2 (3)
where
R = resulting force on the bend (N)
Example - Resulting force on a bend due to mass flow and flow velocity
The resulting force on a 45o bend with
- internal diameter 102 mm = 0.102 m
- water with density 1000 kg/m3
- flow velocity 20 m/s
can be calculated by as
Resulting force in x-direction:
Rx = (1000 kg/m3) π ((0.102 m) / 2)2 (20 m/s)2 (1 - cos(45))
= 957 N
Resulting force in y-direction:
Ry = (1000 kg/m3) π ((0.102 m) / 2)2 (20 m/s)2 sin(45)
= 2311 N
Resulting force on the bend
R = (957 N)2 + (2311 N)2)1/2
= 2501 N
Note - if β is 90othe resulting forces in x- and y-directions are the same.
Resulting force due to Static Pressure
The pressure "acting" on the end surfaces of the bend creates resulting forces in x- and y-directions.
The resulting force in x-direction can be expressed as
Rpx = p A (1- cos(β)) (4)
= p π (d / 2)2 ( 1- cos(β)) (4b)
where
Rpx = resulting force due to pressure in x-direction (N)
p = gauge pressure inside pipe (Pa, N/m2)
The resulting force in y-direction can be expressed as
Rpy = p π (d / 2)2 sin(β) (5)
where
Rpy = resulting force due to pressure in y-direction (N)
The resulting force on the bend due to force in x- and y-direction can be expressed as:
Rp = (Rpx2 + Rpy2)1/2 (6)
where
Rp = resulting force on the bend due to static pressure (N)
Example - Resulting force on a bend due to pressure
The resulting force on a 45o bend with
- internal diameter 102 mm = 0.102 m
- pressure 100 kPa
can be calculated by as
Resulting force in x-direction:
Rx = (100×103 Pa) π ((0.102 m) / 2)2 (1 - cos(45))
= 239 N
Resulting force in y-direction:
Ry = (100×103 Pa) π ((0.102 m) / 2)2 sin(45)
= 578 N
Resulting force on the bend
R = ((239 N)2 + (577 N)2)1/2
= 625 N