Parts per Million - ppm
ppm - or parts per million - is commonly used as a unit of concentration.
Parts per million - ppm - is commonly used as a dimensionless measure of small levels (concentrations) of pollutants in air, water, body fluids, etc.
Parts per million is the molar mass, volume or mass ratio between the pollutant component and the solution. ppm is defined as
ppm = 1,000,000 c / s
= 106 c / s (1)
where
c = molar mass, volume or mass of the solute component (mole, m3, ft3, kg, lbm)
s = molar mass, volume or mass of the solution (mole, m3, ft3, kg, lbm)
In the metric system ppm for mass can be expressed in terms of milligram versus kg where
- 1 mg/kg = 1 part per million
ppm can be also be expressed as
- 1 ppm = 10-6 = 0.0001 % = 0.001 ‰
- 1 000 ppm = 0.1 %
- 10 000 ppm = 1%
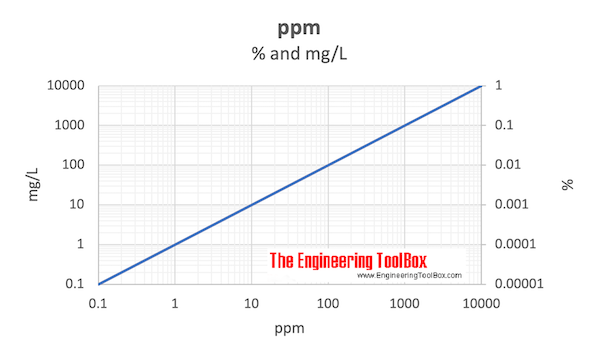
Download and print ppm vs. percent and mg/L chart
Alternatively - mass related units to measure very small concentration levels:
- ppb - parts per billion (1 / 1,000,000,000 or 10-9)
- ppt - parts per trillion (1 / 1,000,000,000,000 or 10-12)
- ppq - parts per quadrillion (1 / 1,000,000,000,000,000 or 10-15)
An alternatively mass related unit to measure larger concentration levels is weight percent which can be expressed as
weight percent = 100 mc / ms (2)
ppm vs. Mass per Unit Volume
The concentration of a component can be measured as mass per unit volume - like mg/liter, mg/cm 3 etc.
Weight of substance added to one unit volume of water to give one part per million (ppm)
1 ppm
= 2.72 pounds per acre-foot
= 1,233 grams per acre-foot
= 1.233 kilograms per acre-foot
= 0.0283 grams per cubic foot
= 0.0000624 pounds per cubic foot
= 0.0038 grams per U.S. gallon
= 0.058419 grains per U.S. gallon
= 0.07016 grains per Imperial gallon
= 1 milligram per liter (mg/L)
= 1 microlitre ( μL) per liter
= 0.001 gram per litre
= 8.345 pounds per million gallons of water
Example - Volume Concentration of Carbon Dioxide in Air
The concentration of carbon dioxide in air is aprox. 400 ppm . The volume of carbon dioxide in one 1 m3 of air can be calculated by modifying (1) to
c = ppm s / 106
= (400 ppm) (1 m3) / 106
= 0.0004 m3/m3
Percent by Volume
Volume percent can be expressed as volume per unit volume:
percent by volume = 100 vc / (vc + vs ) (3)
where
vc = volume component
vs = volume solvent
Molarity
Molarity is the number of moles of solute (substance of interest - pollution, etc.) dissolved in one liter (volume) of the solution.
Molality
Molality is the number moles of solute divided by kilograms of solvent.



