Electrical Conductivity - Elements and other Materials
Electric conductance is the ability of a element to conduct an electric current.
- Conductors are materials with loosely attached valence electrons - electrons can drift freely between the atoms
- Insulators have structures where the electrons are bound to the atoms by ionic or covalent bonds - almost no current can flow
- Semiconductors are insulating materials where the bonds can be broken with applied voltage - electrons can be released and moved from one vacated valence site to another.
Electrical Conductivity
Electrical conductivity or specific conductivity is the measure of a material's ability to conduct electric current. Conductivity is the reciprocal (inverse) of electrical resistivity.
Electrical conductivity is defined as the ratio of the current density to the electric field strength and can be expressed as
σ = J / E (1)
where
σ = electrical conductivity (1/ohms m, 1/Ω m, siemens/m, S/m, mho/m)
J = current density (amps/m2)
E = electric field strength (volts/m)
One siemens - S - is equal to the reciprocal of one ohm and is also referred to as one mho.
Electrical Conductivity of some Common Materials
| Product | Electrical Conductivity - σ - (1/Ω m, S/m, mho/m) |
|---|---|
| Aluminum | 37.7×106 |
| Beryllium | 31.3×106 |
| Cadmium | 13.8×106 |
| Calcium | 29.8×106 |
| Chromium | 7.74×106 |
| Cobalt | 17.2×106 |
| Copper | 59.6×106 |
| Copper - annealed | 58.0×106 |
| Gallium | 6.78×106 |
| Gold | 45.2×106 |
| Iridium | 19.7×106 |
| Iron | 9.93×106 |
| Indium | 11.6×106 |
| Lithium | 10.8×106 |
| Magnesium | 22.6×106 |
| Molybdenum | 18.7×106 |
| Nickel | 14.3×106 |
| Niobium | 6.93×106 |
| Osmium | 10.9×106 |
| Palladium | 9.5×106 |
| Platinum | 9.66×106 |
| Potassium | 13.9×106 |
| Rhenium | 5.42×106 |
| Rhodium | 21.1×106 |
| Rubidium | 7.79×106 |
| Ruthenium | 13.7×106 |
| Silver | 63×106 |
| Sodium | 21×106 |
| Strontium | 7.62×106 |
| Tantalum | 7.61×106 |
| Technetium | 6.7×106 |
| Thallium | 6.17×106 |
| Thorium | 6.53×106 |
| Tin | 9.17×106 |
| Tungsten | 18.9×106 |
| Zinc | 16.6×106 |
| Seawater | 4.5 - 5.5 |
| Water - Drinking | 0.0005 - 0.05 |
| Water - Deionized | 5.5×10-6 |
- 1 S/m = 104 μS/cm = mho/m
- 1 S/cm = 10-2 S/m
- 1 1/Ω m = S/m = 3.28 1/Ω ft = 3.28 S/ft
Electrical Conductivity of Elements relative to Silver
| Element | Electrical Conductivity relative to Silver (%) |
|---|---|
| Silver | 100.0 |
| Copper | 94.6 |
| Gold | 71.7 |
| Aluminum | 59.8 |
| Beryllium | 49.7 |
| Calcium | 47.3 |
| Magnesium | 35.9 |
| Rhodium | 33.5 |
| Sodium | 33.0 |
| Barium | 30.6 |
| Tungsten | 30.0 |
| Molybdenum | 29.7 |
| Cobalt | 27.3 |
| Zinc | 26.3 |
| Nickel | 22.6 |
| Cadmium | 21.9 |
| Ruthenium | 21.7 |
| Cesium | 20.0 |
| Indium | 18.4 |
| Osmium | 17.3 |
| Lithium | 17.1 |
| Uranium | 16.5 |
| Manganese | 15.8 |
| Iron | 15.8 |
| Platinum | 15.3 |
| Palladium | 15.1 |
| Tin | 14.6 |
| Titanium | 13.7 |
| Iridium | 13.5 |
| Rubidium | 12.4 |
| Chromium | 12.3 |
| Tantalum | 12.1 |
| Steel | 12.0 |
| Thallium | 9.8 |
| Lead | 8.4 |
| Columbium | 5.1 |
| Vanadium | 5.0 |
| Arsenic | 4.9 |
| Antimony | 3.6 |
| Mercury | 1.8 |
| Bismuth | 1.4 |
| Tellurium | 0.0 |
Electrical Conductivity of Highly Purified Water

Electrical Resistivity
Conductivity is the reciprocal (inverse) of electrical resistivity. Electrical resistivity can be expressed as
ρ = 1 / σ (2)
where
ρ = electrical resistivity (ohm m2/m, ohm m)
Resistance of a Conductor
The resistance for a conductor can be expressed as
R = ρ l / A (3)
where
R = resistance (ohms, Ω)
l = length of conductor (m)
A = cross sectional area of conductor (m2)
Example - Resistance of a Wire
The resistance of 1000 m copper wire gauge #10 with cross sectional area 5.26 mm2 can be calculated as
R = (1.724×10-8 ohm m2/m) (1000 m) / ((5.26 mm2) (10-6 m2/mm2))
= 3.2 ohm
Resistivity and Conductivity Conversion
| Grains/gal as CaCO3 | ppm as CaCO3 | ppm NaCl | Conductivity μmho/cm | Resistivity MΩ/cm |
|---|---|---|---|---|
| 99.3 | 1700 | 2000 | 3860 | 0.00026 |
| 74.5 | 1275 | 1500 | 2930 | 0.00034 |
| 49.6 | 850 | 1000 | 1990 | 0.00050 |
| 24.8 | 425 | 500 | 1020 | 0.00099 |
| 9.93 | 170 | 200 | 415 | 0.0024 |
| 7.45 | 127 | 150 | 315 | 0.0032 |
| 4.96 | 85.0 | 100 | 210 | 0.0048 |
| 2.48 | 42.5 | 50 | 105 | 0.0095 |
| 0.992 | 17.0 | 20 | 42.7 | 0.023 |
| 0.742 | 12.7 | 15 | 32.1 | 0.031 |
| 0.496 | 8.50 | 10 | 21.4 | 0.047 |
| 0.248 | 4.25 | 5.0 | 10.8 | 0.093 |
| 0.099 | 1.70 | 2.0 | 4.35 | 0.23 |
| 0.074 | 1.27 | 1.5 | 3.28 | 0.30 |
| 0.048 | 0.85 | 1.00 | 2.21 | 0.45 |
| 0.025 | 0.42 | 0.50 | 1.13 | 0.88 |
| 0.0099 | 0.17 | 0.20 | 0.49 | 2.05 |
| 0.0076 | 0.13 | 0.15 | 0.38 | 2.65 |
| 0.0050 | 0.085 | 0.10 | 0.27 | 3.70 |
| 0.0025 | 0.042 | 0.05 | 0.16 | 6.15 |
| 0.00099 | 0.017 | 0.02 | 0.098 | 10.2 |
| 0.00070 | 0.012 | 0.015 | 0.087 | 11.5 |
| 0.00047 | 0.008 | 0.010 | 0.076 | 13.1 |
| 0.00023 | 0.004 | 0.005 | 0.066 | 15.2 |
| 0.00012 | 0.002 | 0.002 | 0.059 | 16.9 |
- grains/gal = 17.1 ppm CaCO3
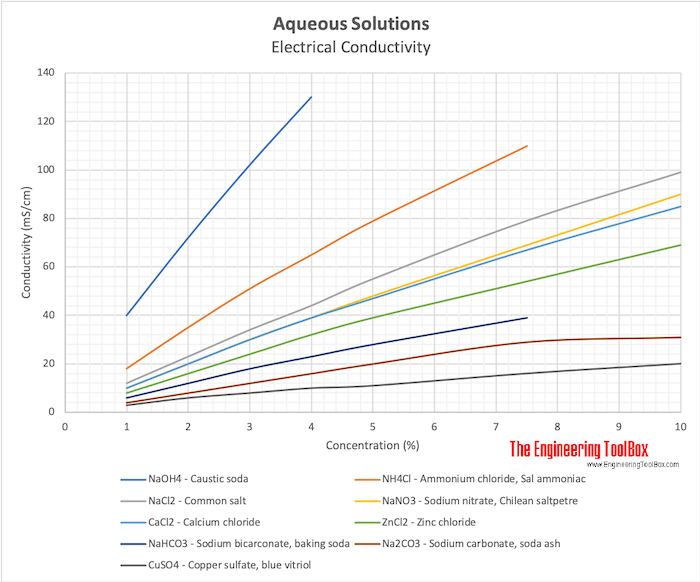
Electrical Conductivity of Aqueous Solutions
Electrical conductivity of aqueous solutions like
- NaOH4 - Caustic soda
- NH4 Cl - Ammonium chloride, Sal ammoniac
- NaCl2- Common salt
- NaNO3 - Sodium nitrate, Chilean saltpetre
- CaCl2- Calcium chloride
- ZnCl2- Zinc chloride
- NaHCO3 - Sodium bicarconate, baking soda
- Na2CO3 - Sodium carbonate, soda ash
- CuSO4 - Copper sulfate, blue vitriol