Capacitors - Parallel and Serial Circuits
Parallel and serial connected capacitor circuits.
Capacitors in Parallel
Capacitors can be connected in parallel:
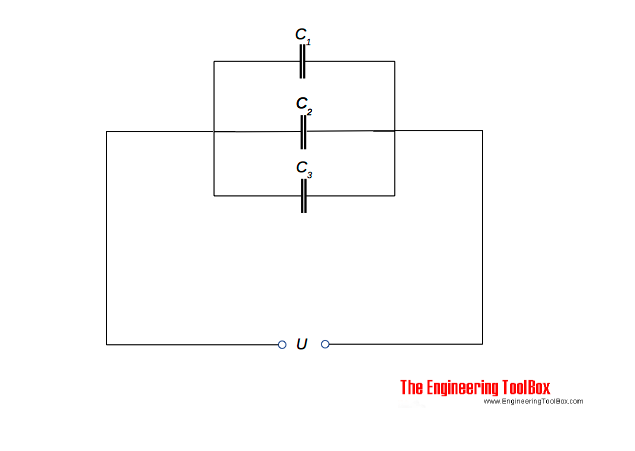
The equivalent capacitance for parallel-connected capacitors can be calculated as
C = C1 + C2 + . . + Cn (1)
where
C = equivalent capacitance for the parallel connected circuit (Farad, F, μF)
C1..n = capacitance capacitors (farad, F, μF)
It is common to use µF as the unit for capacitance.
Capacitors in Series
Capacitors can be connected in series:
The equivalent capacitance for series-connected capacitors can be calculated as
1 / C = 1 / C1 + 1 / C2 + . . + 1 / Cn (2)
For the special case with two capacitors in series - the capacitance can be expressed as
1 / C = ( C1 + C2) / (C1 C2) (2b)
- or transformed to
C = C1 C2 / (C1 + C2) (2c)
Example - Capacitors Connected in Parallel and in Series
The equivalent capacitance of two capacitors with capacitance 10 μF and 20 μF can be calculated as
in parallel
C = (10 μF) + (20 μF)
= 30 μF
in series
1 / C = 1 / (10 μF) + 1 / (20 μF)
= 0.15 1/μF
or
C = 1 / 0.15 (1/μF)
= 6.7 μF
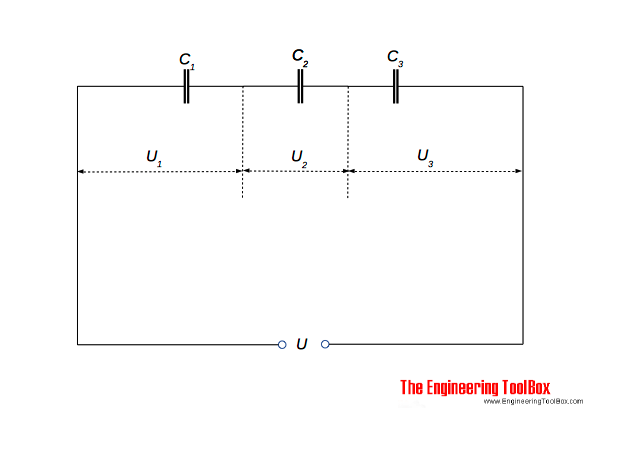
Capacitors in Series
Three capacitors C1 = 3 μF, C2= 6 μF and C3 = 12 μF are connected in series as indicated in the figure above. The voltage supply to the circuit is 230 V.
The equivalent circuit capacitance can be calculated with (2)
1 / C = 1 / (3 μF) + 1 / (6 μF) + 1 / (12 μF)
= (4 + 2 + 1) / 12
= 0.58 1/μF
- or transformed
C = 12 / (4 + 2 + 1)
= 1.7 μF
The total charge in the circuit can be calculated with
Q = U C
where
Q = charge (coulomb, C)
U = electric potential (V)
- or with values
Q = (230 V) (1.7×10-6 F)
= 3.91×10-4 C
= 391 μC
Since the capacitors are connected in series - the charge is 391 μC on each of them.
The voltage across capacitor 1 can be calculated
U1 = Q / C1
= (391 μC) / (3 μF)
= 130 V
The voltage across capacitor 2 can be calculated
U2= Q / C2
= (391 μC) / (6 μF)
= 65 V
The voltage across capacitor 3 can be calculated
U3 = Q / C3
= (391 μC) / (12 μF)
= 33 V
Capacitance of Two Coaxial Cylinders
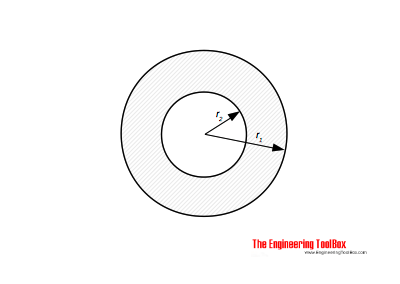
The capacitance of two coaxial cylinders as indicated in the figure can be calculated as
C = 2 π εo εr l / ln(r2 / r1) (3)
where
εo = absolute permittivity, vacuum permittivity (8.85×10-12 F/m, farad/m)
l = length of cylinders
r2= radius of inner cylinder
r1 = radius of outer cylinder



