Signals - Adding Decibels
The logarithmic decibel scale is convenient when adding signal values like sound power, pressure and others from two or more sources.
The decibel (dB) is a logarithmic unit used to express the ratio of two signal values - like power, sound power or pressure, voltage, intensity etc. - where one value is a reference value.
Adding Equal Signal Levels
The total signal level in decibel from equal signal sources can be calculated as
Lt = 10 log (n S / Sref)
= 10 log (S / Sref) + 10 log (n)
= Ls + 10 log (n) (1)
where
Lt = total signal level (dB)
S = signal (signal unit)
Sref = signal reference (signal unit)
n = number of sources
Ls = signal level from each single source (dB)
The signal units depends on the nature of the signal - W for power, Pa for pressure and so on.
Note! - adding sound pressure levels.
Example - Total Sound Power from Two Identical Fans
For sound power it is common to use 10-12 W as the reference sound power. Total sound power from two identical fans each generating 1 W in noise power can be calculated as
Lt = 10 log (2 (1 W) / (1 10-12 W))
= 123 dB
Sound power and sound power level are often used to specify the noise or sound emitted from technical equipment like fans, pumps or other machines. The "sound" measured with microphones or sensors (meters) are sound pressure.
Adding Equal Signals Units Calculator
S - signal (signal unit)
Sref - signal reference (signal unit)
n - number of signal sources
Adding Equal Signal Levels (decibels) Calculator
Ls - signal level from single source (decibel, dB)
n - number of signal sources
Adding equal signal sources can be expressed graphically
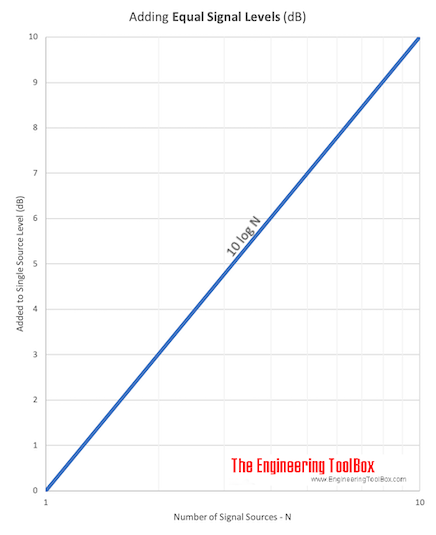Download and print Adding Signal Level of Equal Sources chart.
Note! Adding two identical sources (doubling the signal) will increase the total signal level with 3 dB (10 log(2)).
| Number of Sources | Increase in Sound Power Level (dB) |
|---|---|
| 2 | 3 |
| 3 | 4.8 |
| 4 | 6 |
| 5 | 7 |
| 10 | 10 |
| 15 | 11.8 |
| 20 | 13 |
Adding Signals from Sources with different Strengths
The total signal level from sources with different strengths can be calculated as
Lt = 10 log ((S1 + S2 ... + Sn) / Sref) (2)
Example - Total Sound Power from Two different Fans
The total noise power from two fans - one with sound power 1 W and the other with sound power 0.5 W - can be calculated as
Lt = 10 log (((1 W) + (0.5 W)) / (1 10-12 W))
= 122 dB
Adding two signal sources with different levels can be expressed graphically in decibels as
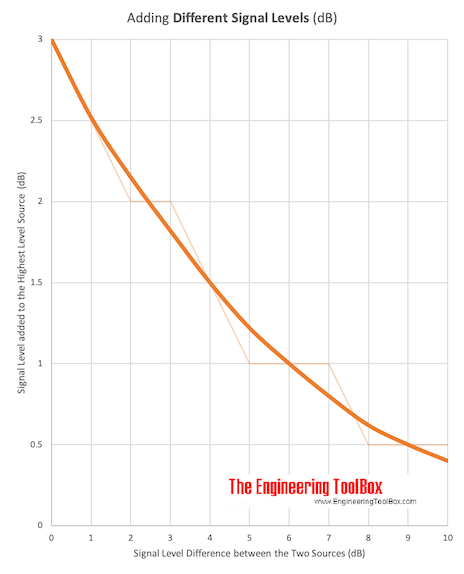
Download and print Adding Sources with different Signal Levels.
| Signal Level Difference between two Sources (dB) | Decibels to Add to the Highest Signal Level (dB) |
|---|---|
| 0 | 3 |
| 1 | 2.5 |
| 2 | 2 |
| 3 | 2 |
| 4 | 1.5 |
| 5 | 1 |
| 6 | 1 |
| 7 | 1 |
| 8 | 0.5 |
| 9 | 0.5 |
| 10 | 0.5 |
| > 10 | 0 |
Example - Adding Sound Power in Decibels
The sound power from one of the fans in the example above can be calculated as
Ls1 = 10 log((1 W) / (1 10-12 W))
= 120 dB
The sound power from the other fan can be calculated as
Ls2 = 10 log((0.5 W) / (1 10-12 W))
= 117 dB
The difference in decibel is
Ls1 - Ls2
= (120 dB) - (117 dB)
= 3 dB
From the table or diagram above a difference of 3 dB requires that 2 dB must be added to the highest sound pressure source as
Lt = (120 dB) + (2 dB)
= 122 dB
