Propagation of Outdoor Sound - Partial Barriers
The transmission of outdoor sound through and around barriers - the Fresnel Number.
If a barrier is interposed between a sound source and a receiver, part of the sound will be
- reflected back from the barrier
- transmitted through the barrier
- diffracted around the barrier
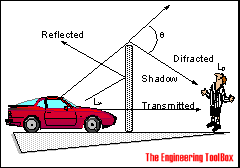
The attenuation can be expressed with the help of the Fresnel number expressed as:
N = 2 δ / λ (1)
where
N = Fresnel number (dimensionless)
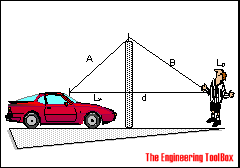
δ = A + B - d, can be calculated from the figure below (m or ft)
λ = wavelength of the sound (m or ft)
Note! The attenuation depends on the wavelength of the sound. For short waves (high frequencies) the Fresnel number limits infinitely. For higher wavelengths the Fresnel number limits to zero.
The outdoor barrier attenuation for different Fresnel number can be estimated with the diagram below.
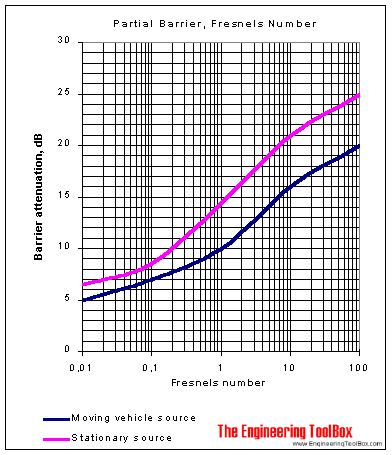
Note! The attenuation is reduced for moving sources (like vehicles etc.) compared to stationary sources.
Example - Attenuation by an Outdoor Highway Noise Barrier
The distance A from a highway to the top of a barrier is 20 m, the distance B from top of the barrier to a person is 30 m and the distance d between the highway and the person is 43 m. The d value can be calculated as
δ = (20 m) + (30 m) - (43 m)
= 7 m
The Fresnels number for noise with frequency 500 Hz ( wavelength 0.69 m) can be calculated as
N = 2 (7 m) / (0.69 m)
= 20
The barrier attenuation for noise with frequency 500 Hz can then be estimated from the diagram above to approximately
17.5 dB
The Fresnels number for noise with frequency 2000 Hz ( wavelength 0.17 m) can be calculated as
N = 2 (7 m) / (0.17 m)
= 82
The barrier attenuation for noise with frequency 2 000 Hz can then be estimated from the diagram above to approximately
20 dB



