Pulleys
Pulleys, blocks and tackles.
A pulley is a device that can increase the magnitude of an effort force .
Without Pulley
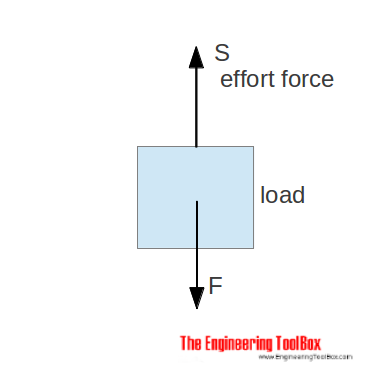
With no pulley - the effort force is similar to the load - in opposite direction.
S = F (1)
where
S = effort force (N, lb)
F = load (N, lb)
Single Pulley
Fixed Pulley
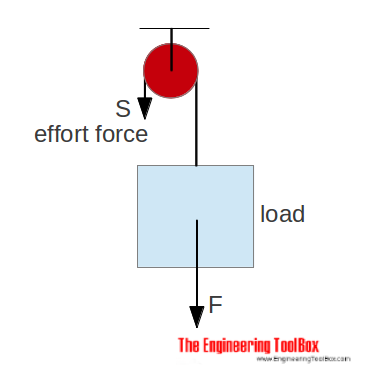
With a single fixed pulley the effort force is similar (or more due to efficiency loss) to the load.
S = F (2)
The advantage with the single fixed pulley is that the direction of force is changed - it is possible to pull down instead of lifting up.
Movable Pulley
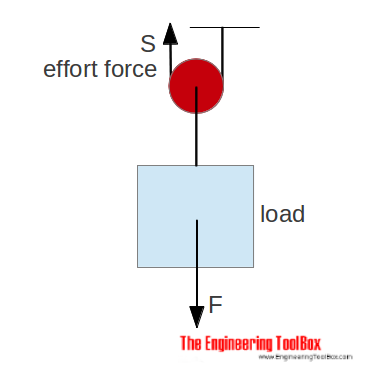
With a single moveable pulley the effort force is half (or more due to efficiency loss) of the load.
S = 1/2 F (3)
Combined Pulleys
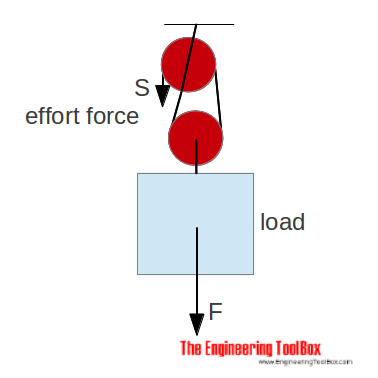
With a combined moveable pulley as above - the effort force is half (or more due to efficiency loss) of the load.
S = 1/2 F (4)
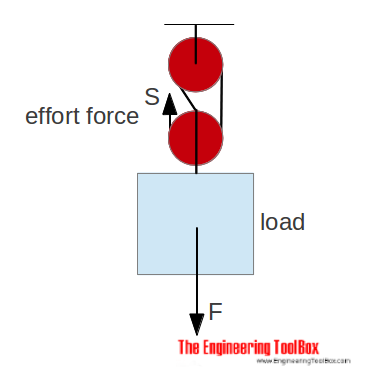
With two pulleys and the ropes as above - the effort force is 1/3 (or more due to efficiency) of the load.
S = 1/3 F (5)
General Equation for Blocks and Tackles
The general effort force equation for a block or tackle to raise or pull a load can be expressed as
S = F / (μ n)
= (m g) / (μ n) (6)
where
S = effort force (N, lb)
F = load (often weight ) (N, lb)
m = mass (kg, slugs ) (when lifting a mass)
g = constant of gravitation (9.81 m/s2, 32.17405 ft/s2) (when lifting a mass)
μ = mechanical efficiency of the system (equal to one for an ideal friction-less system, a fraction less than one for real-world systems with energy losses due to friction)
n = number of ropes between the sets of pulleys
Block, Tackle or Pulley Calculator
The calculator below can be used to calculate effort force in block, tackle or pulley construction. The calculator can be used for metric and imperial units as long as the use of units are consistent.
Note that kg is the SI units for mass - more about mass and weight !
Example - Pulley and Effort Force
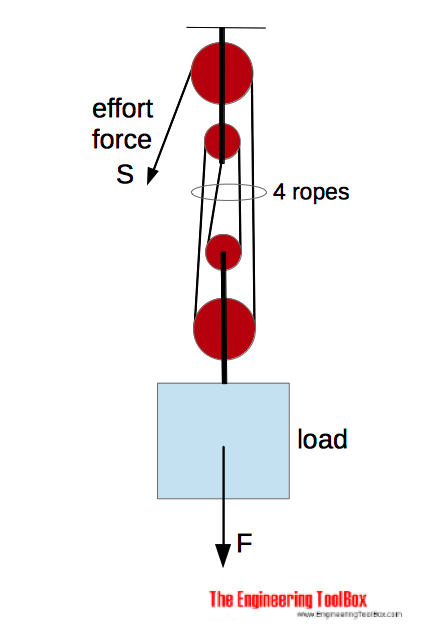
The effort force for a pulley with 4 ropes , friction loss μ = 0.8, and load 100 kg can be calculated as
S = (100 kg) (9.81 m/s2) / ((0.8) (4))
= 307 N
Related Topics
-
Dynamics
Motion of bodies and the action of forces in producing or changing their motion - velocity and acceleration, forces and torque. -
Mechanics
The relationships between forces, acceleration, displacement, vectors, motion, momentum, energy of objects and more.
Related Documents
-
Belt driven Fans - Fan vs. Motor Speed
Fan vs. motor speed in belt driven fans. -
Belt Transmissions - Speed and Length of Belts
Calculate length and speed of belt and belt gearing. -
Belts - Power Transmission and Efficiency
Calculate belts power transmission and efficiency -
Belts - Pulley Diameters vs. Speed
The pulley laws - driver and driven - diameter and rpm -
Bodies Moving on Inclined Planes - Acting Forces
Required forces to move bodies up inclined planes. -
Elevators - Force and Power
Required force and power to lift an elevator. -
Equilibrant Force
The force required to keep a system of forces in equilibrium. -
Force Ratio
The force ratio is the load force versus the effort force. -
Forces and Tensions in Ropes due to Angle
Reduced load capacities in ropes, cables or lines - due to acting angle. -
Friction - Friction Coefficients and Calculator
Friction theory with calculator and friction coefficients for combinations of materials like ice, aluminum, steel, graphite and many more. -
Lifting Wheels
Loads and effort force with lifting wheels. -
Mass vs. Weight
Mass vs. weight - the Gravity Force. -
Motors - Speed vs. Pulley Diameter
Pulley (Sheave) selection charts for motors ranging 850 - 3450 rpm. -
Movement Ratio
Machines and movement ratio (velocity ratio). -
Polyester Polyolefin Ropes - Strengths
Polyester Polyolefin dual fiber 3-strand rope - minimum breaking strength and safe load. -
Polyester Ropes - Strengths
Polyester 3-strand and 8-strand rope - minimum breaking strength and safe load. -
Polypropylene Fiber Ropes - Strengths
Polypropylene fiber 3-strand and 8 strand rope - minimum breaking strength and safe load. -
Shackles - Safe Loads
Safe loads of shackles. -
Sisal Ropes - Strengths
Sisal rope 3-strand, minimum breaking strength and safe load. -
Threaded Rods - Proof Loads - Metric Units
Proof load capacities of metric threaded steel rods. -
Toggle Joint
A toggle joint mechanism can be used to multiply force. -
Winches
Effort force to raise a load. -
Wire Rope Slings
Sling angles and influence on capacity.




