Bodies Moving on Inclined Planes - Acting Forces
Required forces to move bodies up inclined planes.
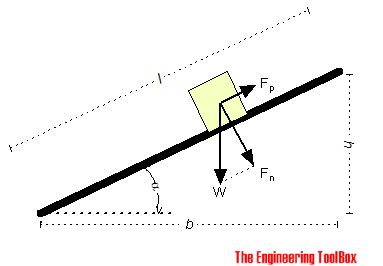
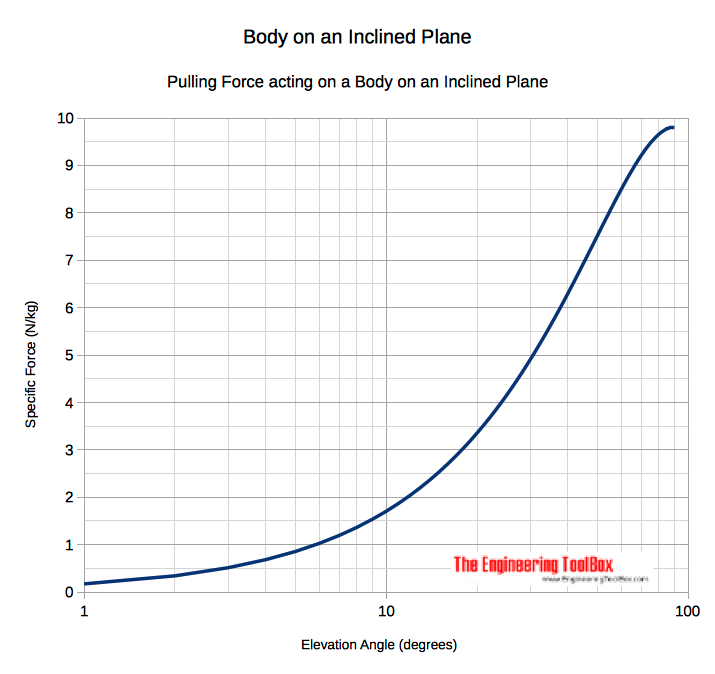
If we neglect friction between the body and the plane - the force required to move the body up an inclined plane can be calculated as
F p = W h / l
= W sin α
= m a g sin α (1)
where
F p = pulling force (N, lb f )
W = m a g
= gravity force - or weight of body (N, lb f )
h = elevation (m, ft)
l = length (m, ft)
α = elevation angle (degrees)
m = mass of body (kg, slugs )
a g = acceleration of gravity (9.81 m/s 2 , 32.174 ft/s 2 )
By adding friction - (1) can be modified to
F p = W (sin α + μ cos α)
= m a g (sin α + μ cos α) (2)
where
Example - Pulling Force on Inclined Plane
A body with mass 1000 kg is located on a 10 degrees inclined plane. The pulling force without friction can be calculated as
F p = (1000 kg) (9.81 m/s 2 ) sin(10°)
= 1703 N
= 1.7 kN
Online Inclined Plane Force Calculator - SI Units
The calculator below can be used to calculate required pulling force to move a body up an inclined plane.
Online Inclined Plane Force Calculator - Imperial Units
Angle of Repose
A body resting on a plane inclined at at an angle α to the horizontal plane is in a state of equilibrium when the gravitational force tending to slide the body down the inclined plane is balanced by an equal and opposite frictional force acting up the inclined plane.
For equilibrium the "angle of response" α can be expressed as:
μ = F p / F n = (W sin α) / (W cos α) = tan α (3)
Example - Gradient Force acting on a Car, Work Done and Power Required
The weight of a Tesla Model X is 2400 kg . The force acting on the car with 5% inclination can be calculated from (1) as
F p_5% = (2400 kg) ( 9.81 m/s 2 ) sin (5°)
= 2051 N
The force acting on the car with 10% inclination can be calculated as
F p_10% = (2400 kg) ( 9.81 m/s 2 ) sin (10°)
= 4088 N
If the Tesla is moving along the inclined roads with the same speed - the work done by the forces after 1 km can be calculated as
W 5% = (2051 N) (1000 m)
= 2051 kJ
W 10% = (4088 N) (1000 m)
= 4088 kJ
If the speed of the Tesla is 80 km/h (22.2 m/s) - the time to drive the distance can be calculated as
t 80 = (1000 m) / (22.2 m/s)
= 45 s
The power required to move the vehicle (without rolling and air resistance) can be calculated as
P 5% = (2051 kJ) / (45 s)
= 45.6 kW
P 50% = (4088 kJ) / (45 s)
= 90.8 kW
If the speed of the car is reduced to 60 km/h (16.6 m/s) - the time to drive the distance can be calculated as
t 60 = (1000 m) / (16.6 m/s)
= 60.2 s
The power required to move the vehicle (without rolling and air resistance) can be calculated as
P 5% = (2051 kJ) / (60.2 s)
= 34.1 kW
P 50% = (4088 kJ) / (60.2 s)
= 67.9 kW
Related Topics
-
Dynamics
Motion - velocity and acceleration, forces and torque. -
Mechanics
Forces, acceleration, displacement, vectors, motion, momentum, energy of objects and more.
Related Documents
-
Acceleration of Gravity and Newton's Second Law
Acceleration of gravity and Newton's Second Law - SI and Imperial units. -
Car - Required Power and Torque
Power, torque, efficiency and wheel force acting on a car. -
Equilibrant Force
The force required to keep a system of forces in equilibrium. -
Force
Newton's third law - force vs. mass and acceleration. -
Force Ratio
The force ratio is the load force versus the effort force. -
Forces acting on Body Moving in a Horizontal Plane
The forces acting on bodies moved in horizontal planes. -
Friction - Friction Coefficients and Calculator
Friction theory with calculator and friction coefficients for combinations of materials like ice, aluminum, steel, graphite and many more. -
Mass vs. Weight
Mass vs. weight - the Gravity Force. -
Pulleys
Pulleys, blocks and tackles. -
Rolling Resistance
Rolling friction and rolling resistance. -
Slope - Degree, Gradient and Grade Calculator
Convert slopes pitch between degrees, gradients and grades. -
Support Reactions - Equilibrium
Static equilibrium is achieved when the resultant force and resultant moment equals to zero. -
Work done by Force
Work done by a force acting on an object.
