Acceleration of Gravity and Newton's Second Law

Acceleration of gravity and Newton's Second Law - SI and Imperial units.

Newton's Second Law

"Change of motion is proportional to the force applied, and take place along the straight line the force acts."

Newton's second law for the gravity force - weight - can be expressed as

W = F_g

= m a_g

= m g (1)

where

W, Fg = weight, gravity force (N, lb_f)

m = mass (kg, slugs)

a_g = g = acceleration of gravity (9.81 m/s², 32.17405 ft/s²)

The force caused by gravity - a_g - is called weight.

Note!

mass is a property - a quantity with magnitude
force is a vector - a quantity with magnitude and direction

The acceleration of gravity can be observed by measuring the change of velocity related to change of time for a free falling object:

a_g = dv / dt (2)

where

dv = change in velocity (m/s, ft/s)

dt = change in time (s)

An object dropped in free air accelerates to speed 9.81 m/s (32.174 ft/s) in one - 1 - second.

a heavy and a light body near the earth will fall to the earth with the same acceleration (when neglecting the air resistance)

Acceleration of Gravity in SI Units

1 a_g = 1 g = 9.81 m/s² = 35.30394 (km/h)/s

Acceleration of Gravity in Imperial Units

1 a_g = 1 g = 32.174 ft/s²= 386.1 in/s²= 22 mph/s

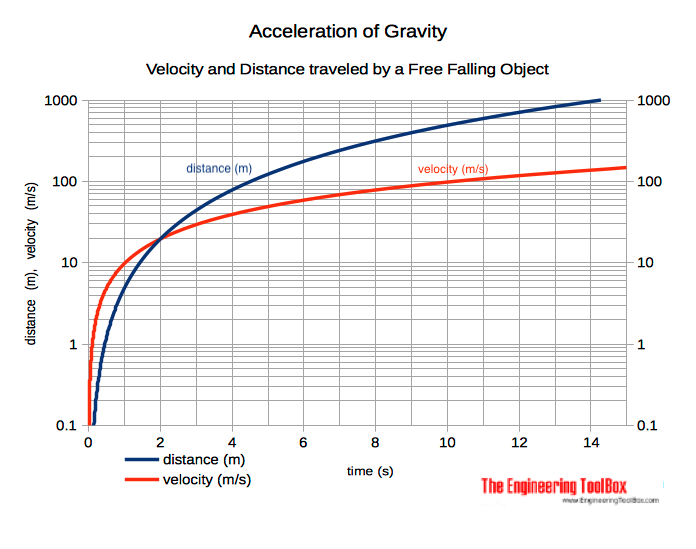
Velocity and Distance Traveled by a Free Falling Object

The velocity for a free falling object after some time can be calculated as:

v = a_g t (3)

where

v = velocity (m/s)

The distance traveled by a free falling object after some time can be expressed as:

s = 1/2 a_g t² (4)

where

s = distance traveled by the object (m)

The velocity and distance traveled by a free falling object:

Time (s)	Velocity				Distance
Time (s)	m/s	km/h	ft/s	mph	m	ft
1	9.8	35.3	32.2	21.9	4.9	16.1
2	19.6	70.6	64.3	43.8	19.6	64.3
3	29.4	106	96.5	65.8	44.1	144.8
4	39.2	141	128.7	87.7	78.5	257.4
5	49.1	177	160.9	110	122.6	402.2
6	58.9	212	193.0	132	176.6	579.1
7	68.7	247	225.2	154	240.3	788.3
8	78.5	283	257.4	176	313.9	1,029.6
9	88.3	318	289.6	198	397.3	1,303.0
10	98.1	353	321.7	219	490.5	1,608.7

Note! Velocities and distances are achieved without aerodynamic resistance (vacuum conditions). The air resistance - or drag force - for objects at higher velocities can be significant - depending on shape and surface area.

Acceleration of gravity on the North and South Pole - and on Equator

Example - Free Falling Stone

A stone is dropped from 1470 ft (448 m) - approximately the height of Empire State Building. The time it takes to reach the ground (without air resistance) can be calculated by rearranging (4):

t = (2 s / a_g)^1/2

= (2 (1470 ft) / (32.174 ft/s²))^1/2

= 9.6 s

The velocity of the stone when it hits the ground can be calculated with (3):

v = (32.174 ft/s²) (9.6 s)

= 308 ft/s

= 210 mph

= 94 m/s

= 338 km/h

Example - A Ball Thrown Straight Up

A ball is thrown straight up with an initial velocity of 25 m/s. The time before the ball stops and start falling down can be calculated by modifying (3) to

t = v / a_g

= (25 m/s) / (9.81 m/s²)

= 2.55 s

The distance traveled by the ball before it turns and start falling down can be calculated by using (4) as

s = 1/2 (9.81 m/s²) (2.55 s)²

= 31.8 m

Newton's First Law

"Every body continues in a state of rest or in a uniform motion in a straight line, until it is compelled by a force to change its state of rest or motion."

Newton's Third Law

"To every action there is always an equal reaction - if a force acts to change the state of motion of a body, the body offers a resistance equal and directly opposite to the force."

Common Expressions

superimposed loads: kN/m²
mass loads: kg/m² or kg/m³
stress: N/mm²
bending moment: kNm
shear: kN

1 N/mm = 1 kN/m
1 N/mm² = 10³ kN/m²
1 kNm = 10⁶ Nmm

Latitude and Acceleration of Gravity

Acceleration of gravity varies with latitude - examples:

Location	Latitude	Acceleration og Gravity (m/s²)
North Pole	90° 0'	9.8321
Anchorage	61° 10'	9.8218
Greenwich	51° 29'	9.8119
Paris	48° 50'	9.8094
Washington	38° 53'	9.8011
Panama	8° 55'	9.7822
Equator	0° 0'	9.7799